 [RL] Dealing with inaccurate models
[RL] Dealing with inaccurate models
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 이전 포스트들을 통해서 얘기한 내용은 결국 model을 활용해서 planning을 할 수 있어서 sampling efficiency도 높이고, 효율적으로 policy를 학습할 수 있다고 했었다. 여기서 던질 수 있는 질문은 "그럼 정확하지 않은(inaccurate) model로 planning 등을 수행하면 policy를 improve할 수 있을까?" 이다. 예를 들어서 앞에서 다뤘던 maze example 상에서도 policy를 improve시키기 위해서는 가능한한 많은 state와 action을 취해서 얻은 value function이 있어야 하는데, 아무래도 exploration도 하고 중간..
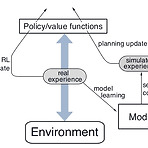 [RL] Dyna as a formalism for planning
[RL] Dyna as a formalism for planning
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 이전 포스트를 통해서 강화학습 상에서의 Model의 정의에 대해서 소개하고, Model을 통해서 생성한 simulated experience를 바탕으로 model을 update하는 Planning에 대해서 다뤘다. 사실 이런 planning과정과 별개로 실제 environment로부터 얻은 experience를 바탕으로 update하는 것을 Direct RL이라고 표현한다. 이번 포스트에서 소개할 Dyna algorithm (sutton)은 앞에서 소개된 Planning과 Direct RL이 결합된 형태로 되어 있다. 우선 기존의 Q-learning과 마찬가지로 실제 environment로부터 e..
 [RL] Model & Planning
[RL] Model & Planning
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 강화학습을 공부하다보면 state나 action같은 기본 notation만큼이나 자주 나오는 단어가 Model이 아닐까 생각된다. 이전 포스트에서 Monte Carlo method나 Temporal Difference Learning을 다뤘고, 이 둘의 차이가 여러가지가 있지만, 그래도 넓은 관점에서 보자면 두 알고리즘은 Model이 있냐(Model-based) 없냐(Model-free)로 나눠서 볼 수 있다. sutton 책에 있는 표현을 가져오자면 Model-based RL은 planning에 초점이 맞춰져 있고, Model-free RL은 learning에 중점을 두고 있다. 그럼 여기서 말..
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 이전 포스트를 통해 배울 수 있었던 것은 크게 다음과 같다. Episode가 끝나야 Value function을 update할 수 있었던 Monte Carlo Method와 다르게 TD Learning은 BootStrapping 기법을 사용해서 Value function을 update할 수 있었다. TD Learning 중에서도 Target Policy와 Behavior Policy의 일치여부에 따라서 On-policy method인 SARSA와 Off-policy method인 Q-learning으로 나눠볼 수 있다. 아무튼 두가지 방법 모두 state action value를 활용한 Bellm..
 [Book] 게임으로 즐겁게 배우는 "게임으로 익히는 코딩 알고리즘"
[Book] 게임으로 즐겁게 배우는 "게임으로 익히는 코딩 알고리즘"
요새 기술 트렌드가 인공지능이라고 많이 표현하고, 회사나 학교에서도 이를 응용한 교육이나 기술을 많이 적용하려고 노력하는 것 같다. 그런데 개인적인 생각으로는 이런 기술도 기본적인 소양이 뒷받침되어야 진정으로 이해하고 나아갈 수 있지 않을까 하는 생각을 많이 해본다. 예를 들어서 행렬연산이나 벡터의 개념없이는 신경망이 연산하고, 학습되는 과정을 이해하기 어려울 것이고, 기본 자료구조나 알고리즘에 대한 이해없이는 그런 동작 과정을 개선시키거나, 이해하는 것 자체가 벅찰 것이다. 사실 나같은 경우도 현업에서 인공지능 관련 기술을 실제 환경에 적용하는 일을 하고 있긴 하지만, 그런 과정이 쉽지 않을 뿐더러 너무나 논리적으로 설명하기 어려운 부분이 많다는 것을 많이 느낀다. 그래서 그냥 시간나는 틈틈히 알고리즘..
 [RL] Q-learning: Off-policy TD Control
[RL] Q-learning: Off-policy TD Control
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 사실 Q-learning에 대해서는 옛날에 한 포스트를 통해서 다뤘었는데, 다시 정리를 해보고자 한다. 일단 알고리즘은 아래와 같다. 이전 포스트에서 다뤘던 SARSA와 거의 비슷한데, 한가지 다른 부분이 바로 Value function을 update하는 부분이다. 다시 한번 SARSA의 update 부분을 살펴보자. $$ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (\color{red}{R_{t+1}} + \color{red}{\gamma Q(S_{t+1}, A_{t+1})} - Q(S_t, A_t)) $$ 그런데 위의 식은 사실 Dynamic Programm..
 [RL] SARSA : GPI with TD
[RL] SARSA : GPI with TD
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 이전 포스트 중에 Generalized Policy Iteration (GPI)에 대해서 다뤘던 내용이 있다. GPI는 현재 policy \(\pi\)에 대한 state value function을 구하는 Policy Evaluation과 해당 state value function을 바탕으로 greedy action을 취함으로써 해당 policy를 개선시키는 Policy Improvement 과정으로 나뉘어져 있다. 그 포스트에서는 Monte Carlo를 사용한 GPI를 소개했었다. 그런데 이제 TD Learning을 살펴봤으니, Monte Carlo method가 Episode가 terminat..
 [RL] Introduction to Temporal Difference Learning
[RL] Introduction to Temporal Difference Learning
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 이전 포스트에서는 Off-policy 방식의 Monte Carlo Prediction에 대해서 다뤘다. 일단 Monte Carlo의 특성상 policy에 대한 trajectory를 여러개 뽑아서 expectation을 취해야 한다. $$ v_{\pi}(s) \doteq \mathbb{E}_{\pi}[ \color{red}{G_t} | S_t=s] $$ 일단 위처럼 State value function을 구하기 위해서는 해당 state \(s\)에서의 total expected return \(G_t\)을 구해야 하고, 이때 Policy Evaluation에선 다음과 공식을 통해서 state val..
 [RL] Off-policy Learning for Prediction
[RL] Off-policy Learning for Prediction
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) 이전 포스트에서는 Monte Carlo method를 Policy Iteration에 적용하기 위해서 필요한 Exploration policy 중 하나인 \(\epsilon\)-soft policy를 소개했다. 그러면서 참고로 소개한 내용 중에 On-policy와 Off-policy라는 것이 있었다. 이 중 Off-policy에 초점을 맞춰서 다뤄보고자 한다. 잠깐 설명이 되었던 바와 같이, On-policy는 action을 선택하는 policy를 직접 evaluate하고, improve시키는 방식을 말한다. 반대로 Off-policy는 action을 선택하는 policy와는 별개로 별도의 pol..
 [RL] Exploration Methods for Monte Carlo
[RL] Exploration Methods for Monte Carlo
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다) Monte Carlo Control의 알고리즘을 보면 초기에 state와 action을 random하게 주는 Exploring Starts (ES)가 반영되어 있는 것을 확인할 수 있었다. 이 방법은 Optimal Policy를 찾는데 적합한 알고리즘일까? 사실 초기 state와 action을 random하게 주는 이유는 policy를 update하는데 있어 필요한 State-Action Value Function을 확보하기 위함이었고, 처음이 지난 이후에는 처음에 설정된 policy \(\pi\)에 따라 움직이는 이른바 deterministic policy이다. 분명 State-Action Va..
 [RL] Monte Carlo for Control
[RL] Monte Carlo for Control
(해당 포스트는 Coursera의 Sample-based Learning Method의 강의 요약본입니다) 일단 State Value Function을 이용한 Monte Carlo Method는 다음과 같이 정의가 된다. $$ V_\pi(s) \doteq \mathbb{E}_{\pi}[G_t | S_t = s] $$ 사실 State Value Function와 State-Action Value Function의 관계는 다음과 같이 정의되어 있기 때문에, $$ V_{*}(s) = \max_{a} Q_{*}(s,a) $$ 이를 활용해보면 다음과 같은 식도 구할 수 있다. $$ q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a] $$ 결국 위 식의 의..
 [RL] What is Monte Carlo?
[RL] What is Monte Carlo?
(해당 포스트는 Coursera의 Sample-based Learning Method의 강의 요약본입니다) Policy Evaluation이나 Policy Improvement는 내부적으로 value function \(V(s)\)를 구할 때 transition probability \(p(s', r| s, \pi(s))\)를 활용했고, 이를 Dynamic Programming을 통해서 구했다. 그런데 생각해보면 알겠지만, 보통 강화학습을 구할 때, 이 transition probability를 아는 상태에서 학습을 시키는 경우는 거의 드물다. 이 Probability를 Dynamic Programming을 통해서 구하는 것은 어렵기 때문에, 보통은 estimation을 통해서 구하는데, 이때 많이 활용..
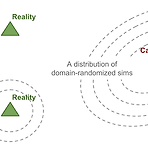 [RL] Domain Randomization for Sim2Real Transfer
[RL] Domain Randomization for Sim2Real Transfer
(해당 글은 OpenAI Engineer인 Lilian Weng의 포스트 내용을 원저자 동의하에 번역한 내용입니다.) Domain Randomization for Sim2Real Transfer If a model or policy is mainly trained in a simulator but expected to work on a real robot, it would surely face the sim2real gap. Domain Randomization (DR) is a simple but powerful idea of closing this gap by randomizing properties of the training environ lilianweng.github.io 만약 model이나 ..
 [RL] Flexibility of the Policy Iteration Framework
[RL] Flexibility of the Policy Iteration Framework
(해당 포스트는 Coursera의 Fundamentals of Reinforcement Learning의 강의 요약본입니다) Policy Iteration은 Policy Evaluation과 Policy Improvement를 반복하면서 현재의 policy \(\pi\)를 최대한 optimal policy \(\pi_*\)에 가깝게 update하는 방법을 말한다. 아마 Sutton책에서는 다음과 같은 그림으로 도식화를 해놨을 것이다. 아니면 이런 그림도 같이 보았을 것이다. 현재의 policy \(\pi\)와 초기의 value function \(v\)가 있으면, 처음에는 \(\pi\)에 따라 action을 취하고 이에 맞게 value function을 update하게 된다 (\(v=v_{\pi}\)) ..
- Total
- Today
- Yesterday
- reward
- RL
- Pipeline
- 한빛미디어
- Windows Phone 7
- Off-policy
- 강화학습
- processing
- PowerPoint
- 파이썬
- End-To-End
- arduino
- Kinect SDK
- Kinect
- Variance
- bias
- TensorFlow Lite
- windows 8
- Distribution
- DepthStream
- SketchFlow
- Policy Gradient
- Expression Blend 4
- dynamic programming
- ai
- 딥러닝
- ColorStream
- Kinect for windows
- Gan
- Offline RL
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |

