티스토리 뷰
(해당 포스트는 Coursera의 Sample-based Learning Method의 강의 요약본입니다)
일단 State Value Function을 이용한 Monte Carlo Method는 다음과 같이 정의가 된다.
$$ V_\pi(s) \doteq \mathbb{E}_{\pi}[G_t | S_t = s] $$
사실 State Value Function와 State-Action Value Function의 관계는 다음과 같이 정의되어 있기 때문에,
$$ V_{*}(s) = \max_{a} Q_{*}(s,a) $$
이를 활용해보면 다음과 같은 식도 구할 수 있다.
$$ q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a] $$
결국 위 식의 의미는 현재의 policy \(\pi\)를 따라가면서 나오는 state-action pair를 바탕으로 expected return을 모아서 이에 대한 평균을 구하겠다는 것이다.
여기서 나올 수 있는 질문이 바로 왜 State Value Function을 바로 쓰면 되지, 굳이 State-Action Value Function으로 바꿔서 풀 필요가 있냐는 것이다. 사실 본질적인 답변일 수 있겠지만 우리가 이런 학습을 통해서 구하고자 하는 것은 Expected Return을 최대화할 수 있는 optimal policy를 구하는 것인데, policy 자체가 현재 state에서 어떤 action을 취할지에 대한 의사 결정을 말하는 것이다. 그렇기 때문에 같은 state내에서 다른 action에 대한 정보도 가지고 있어야 어떤 action이 좋은지 나쁜지, 궁극적으로는 \(Q(s,a_1)\)가 \(Q(s, a_2)\) 와 비교해 좋은지 판단할 수 있기 때문에, policy를 학습하는데 있어서는 State Value Function (\(V(s)\))보다 State-Action Value Function(\(Q(s,a)\))이 유용하게 활용될 수 있다.
그럼 아래와 같은 예를 들어보자.

위와 같이 현재 policy \(\pi\)가 deterministic하고, state \(s_0\)에서는 action \(a_2\)를 취하게끔 되어 있다고 해보자. 물론 \(a_2\)를 선택하게 된 이유는 다른 action인 \(a_0, a_1\)을 취할 때의 q-value(\(Q(s_0, a_0), Q(s_0, a_1)\))보다 \(a_2\)를 취할 때의 q-value(\(Q(s_0, a_2)\))가 더 높았기 때문일 것이고, 이로 인해서 State Value Function \(V(s_0)\)은 \(Q(s_0, a_2)\)와 같을 것이다. 하지만 이 policy가 계속 유지된다면, 무조건 state \(s_0\)에서는 action \(a_2\)를 취할 것이고, action \(a_0, a_1\)에 대한 estimation은 얻기 힘들게 된다. 결국 이를 해결하기 위해 필요한 것이 Exploration이다. 현재 state에서 취할 수 있는 action 각각에 대한 value function이 정의되어 있으면 그만큼 policy를 학습하는데 도움이 될 것이다.
그럼 이렇게 도출한 State-Action Value Function을 활용해서 이전 포스트에서 다뤘던 Generalized Policy Iteration (GPI)를 다시 구성해볼 수 있다. 이전 Generalized Policy Iteration에서는 State Value Function을 사용해서 Policy Evaluation과 Policy Improvement를 수행했다.
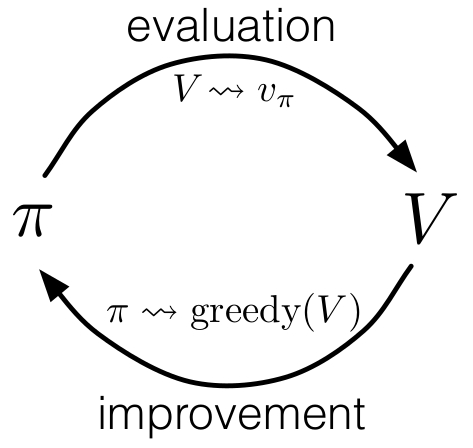
우선 Policy Evaluation에서는 현재의 policy \(\pi\)에 대한 State Value function \(v_{\pi}\)를 만들어주고, Policy Improvement에서 주어진 \(v_{\pi}\)에서 \(v\)를 최대화할 수 있는 greedy action의 집합 \(\pi'\)를 찾는 과정이 Policy Iteration의 개념이었다.

State-Action Value Function을 이용한 Policy Iteration도 앞과 거의 동일하다. 다만 State Value Function 대신 State-Action Value Function을 활용했다는데 차이가 있다. 추가로 Policy Evaluation에서 Monte Carlo method를 반영한 Monte Carlo Prediction이란 방법을 써서, State-Action value를 estimate한다. State-Action Value Function을 활용한 Policy Iteration도 결국 episode별로 policy evaluation과 policy improvement를 반복하면서 현재보다 더 좋은 policy, 궁극적으로는 optimal policy \(\pi_*\)를 찾는 과정을 거치게 된다. 이에 대한 알고리즘은 다음과 같다.

우선 Exploring Starts (ES)라는 개념이 나와있는데, 이 말은 처음 시작할 때는 random하게 state \(s_0\)와 action \(a_0\)를 취하겠다는 것이다. 앞에서 잠깐 언급했던 Exploring이 반영된 것이다. (반대로 처음부터 greedy action을 취하게 된다면, policy improvement를 통해서 optimal policy는 적어질 것이다.) 그리고 한번 action이 취해진 이후로는 policy \(\pi\)를 따르게 된다. 이렇게 state-action pair에 대한 trajectory가 나오면 이를 바탕으로 Policy Iteration이 이뤄지는 것이 Monte Carlo Exploring Starts 이다. 이전의 Policy Iteration에서는 Dynamic Programming을 통해서 각각의 확률도 필요하고, 조금 복잡했었는데, Monte Carlo method를 적용하면서 확률값 대신 sampling에 대한 average를 취하기 때문에 조금더 value function을 구하는 공식이 간결해진 것을 확인할 수 있었다.
'Study > AI' 카테고리의 다른 글
| [RL] Introduction to Temporal Difference Learning (2) | 2019.09.06 |
|---|---|
| [RL] Off-policy Learning for Prediction (3) | 2019.09.05 |
| [RL] Exploration Methods for Monte Carlo (0) | 2019.09.04 |
| [RL] What is Monte Carlo? (0) | 2019.09.02 |
| [RL] Domain Randomization for Sim2Real Transfer (5) | 2019.08.31 |
| [RL] Flexibility of the Policy Iteration Framework (0) | 2019.08.29 |
| [Me][ML] How AI and machine learning are improving customer experience (0) | 2019.08.16 |
- Total
- Today
- Yesterday
- DepthStream
- arduino
- Off-policy
- reward
- Policy Gradient
- End-To-End
- Distribution
- processing
- Offline RL
- PowerPoint
- TensorFlow Lite
- Gan
- windows 8
- bias
- Kinect
- 딥러닝
- Variance
- dynamic programming
- Windows Phone 7
- Kinect for windows
- RL
- 강화학습
- Expression Blend 4
- 파이썬
- SketchFlow
- 한빛미디어
- ColorStream
- Pipeline
- 인공지능
- Kinect SDK
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
