티스토리 뷰
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다)
Monte Carlo Control의 알고리즘을 보면 초기에 state와 action을 random하게 주는 Exploring Starts (ES)가 반영되어 있는 것을 확인할 수 있었다. 이 방법은 Optimal Policy를 찾는데 적합한 알고리즘일까?
사실 초기 state와 action을 random하게 주는 이유는 policy를 update하는데 있어 필요한 State-Action Value Function을 확보하기 위함이었고, 처음이 지난 이후에는 처음에 설정된 policy \(\pi\)에 따라 움직이는 이른바 deterministic policy이다. 분명 State-Action Value Function을 update하는데 도움이 되겠지만, 우리가 마음대로 초기 state와 action을 선택하지 못하는 상황이라면 어떨까? 가령 self-driving과 같은 환경에서 테스트하는 경우, 출발지와 도착지가 명확히 결정되어 있는 상태에서 agent가 마음대로 초기 state와 action을 선택하기 어려울 것이다. 이렇게 exploration Starts를 사용하지 못하는 경우에서는 어떻게 State-Action Value Function을 update할 수 있을까?
Sutton 책에서 Bandit problem을 다뤘던 부분에서 Exploration을 수행하기 위해 나왔던 방법이 \(\epsilon\)-Greedy Policy이었다.
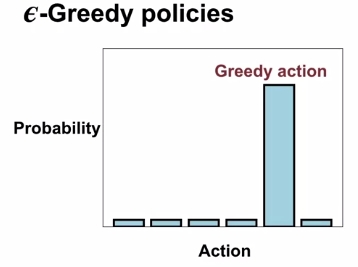
일종의 Stochastic policy 중 하나로써, \(\epsilon\)은 0에서 1사이 값을 가지면서, \(\epsilon\)의 확률만큼 random action을 취하고, 나머지 \(1-\epsilon\)의 확률만큼 Greedy action을 취하는 정책이었다. 사실 이 policy는 특정 확률은 greedy action을 취하겠다는 명확한 rule이 있는 것이지만, 다르게 생각하면 greedy action을 취하지 않고, 다른 방법을 취해볼 수 있다는 생각을 해볼 수 있다. 물론 구현하는 사람 마음이겠지만, 이렇게 확률적인 개념으로 random action을 선택하는 policy를 포괄적으로 \(\epsilon\)-soft policy라고 표현한다. 그래서 쉽게 생각하면 \(\epsilon\)-Greedy policy는 \(\epsilon\)-Soft policy의 subset이라고 보면 좋을 거 같다.
Sutton책에 정의되어 있지만, soft의 의미는 현재의 policy \(\pi\)상에서 모든 \(s \in S, a \in A(s)\)에 대한 \(\pi(a|s) > 0\) 이지만, 점차적으로 optimal한 deterministic policy로 변해간다는 것을 나타낸다.
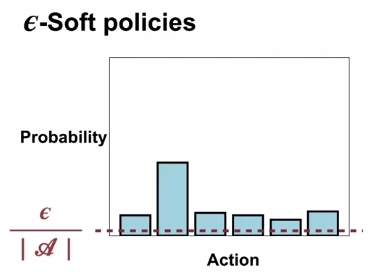
\(\epsilon\)-Soft policy는 기본적으로 모든 action들이 적어도 0이 아닌, \(\frac{\epsilon}{|A|}\) 만큼 취할 확률을 가진다는 전제조건이 붙는다. 물론 어떤 확률은 random하게 더 많이 취해질 수도 있고, 적게 취해질 수도 있겠지만, 그 빈도는 전형적으로 \(\epsilon\)에 따르게 되는 것이다.
일단 이렇게 \(\epsilon\)-Soft policy를 사용함으로써, 이전 Monte Carlo Control에서 사용했던 Exploring Starts는 사용하지 않아도 된다. 즉, 초기 state와 action을 굳이 랜덤하게 선택하지 않더라도, Exploration 효과를 누릴 수 있게 되는 것이다. 그러면 어떤 사람은 "과연 이런 stochastic policy로도 optimal policy를 구할 수 있을까?" 하는 의문을 던질 수 있다. 물론 아는 바와 같이 optimal policy는 deterministic policy이다.
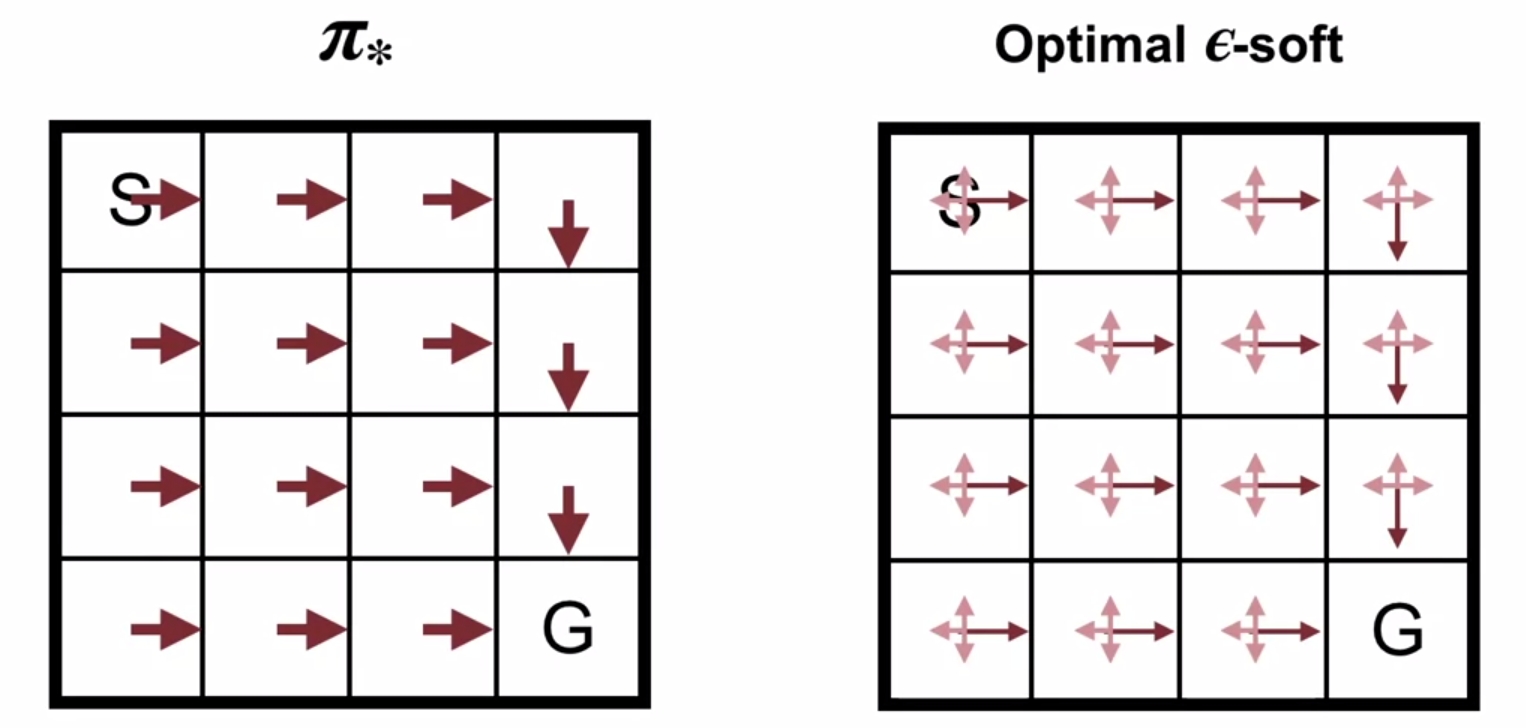
당연히 완전한 optimal policy를 찾을 수는 없다. 그래도 확률적으로는 sub-optimal한 policy를 찾음으로써 일반적인 deterministic policy나 fully-random policy보다 더 좋은 policy를 찾아가는 것이다. 이에 대한 알고리즘은 다음과 같다.

이제 여기서부터는 hyperparameter \(\epsilon\)이 정의되어야 하며, 이에 따로 초기의 policy도 이 \(\epsilon\)에 따라 결정된다. 그 외의 과정은 이전에 다뤘던 Monte Carlo ES와 거의 비슷한데, 한가지 다른 부분이라면 policy Improvement시 update되는 값도 사전에 정의한 \(\epsilon\)의 영향을 받는다는 것이다.
참고로, 알고리즘 설명 중에 나온 용어 중 On-policy란 개념이 있다. On-policy method란 action을 취한 policy (behavior policy) 를 가지고 좋은지 나쁜지 여부를 판단하고, 이를 개선하는 방법을 말한다. 그래서 최종적으로 우리가 구할 policy (target policy)에 맞추는 것을 목표로 한다. 반대로 Off-policy란 개념도 있는데, Off-policy method는 behavior policy와 target policy가 다른 케이스, 다르게 말하면 data를 만들어낸 policy와 개선시킬 policy가 다른 것을 말한다. 그래서 앞에서 다룬 방법들을 대상으로 하자면 Monte Carlo ES method는 같은 policy를 바탕으로 evaluation과 improvement가 이뤄지므로, On-policy Monte Carlo Control method라고 표현할 수 있다. 반대로 Off-policy MC Control method도 있는데, 이는 다음 포스트에서 소개할 예정이다.
'Study > AI' 카테고리의 다른 글
| [RL] SARSA : GPI with TD (3) | 2019.09.11 |
|---|---|
| [RL] Introduction to Temporal Difference Learning (2) | 2019.09.06 |
| [RL] Off-policy Learning for Prediction (3) | 2019.09.05 |
| [RL] Monte Carlo for Control (0) | 2019.09.04 |
| [RL] What is Monte Carlo? (0) | 2019.09.02 |
| [RL] Domain Randomization for Sim2Real Transfer (5) | 2019.08.31 |
| [RL] Flexibility of the Policy Iteration Framework (0) | 2019.08.29 |
- Total
- Today
- Yesterday
- TensorFlow Lite
- SketchFlow
- windows 8
- Pipeline
- ColorStream
- 강화학습
- Distribution
- bias
- RL
- Gan
- Kinect SDK
- 딥러닝
- arduino
- Kinect for windows
- Offline RL
- 파이썬
- ai
- processing
- Windows Phone 7
- Policy Gradient
- End-To-End
- PowerPoint
- Kinect
- 한빛미디어
- Variance
- Off-policy
- dynamic programming
- reward
- Expression Blend 4
- DepthStream
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
