티스토리 뷰
(해당 포스트는 Coursera의 Sample-based Learning Methods의 강의 요약본입니다)
사실 Q-learning에 대해서는 옛날에 한 포스트를 통해서 다뤘었는데, 다시 정리를 해보고자 한다. 일단 알고리즘은 아래와 같다.

이전 포스트에서 다뤘던 SARSA와 거의 비슷한데, 한가지 다른 부분이 바로 Value function을 update하는 부분이다. 다시 한번 SARSA의 update 부분을 살펴보자.
$$ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (\color{red}{R_{t+1}} + \color{red}{\gamma Q(S_{t+1}, A_{t+1})} - Q(S_t, A_t)) $$
그런데 위의 식은 사실 Dynamic Programming에서 잠깐 나왔던 bellman optimality equation과 많은 부분을 공유한다.
$$ q_{\pi}(s, a) = \sum_{s', r} p(s', r|s, a) \big(\color{red}{r} + \color{red}{\gamma} \sum_{a'} \pi(a'|s') \color{red}{q_{\pi}(s', a')} \big) $$
어떻게 보면 state-action value 기반의 bellman equation을 푸는 방식이 결국 SARSA 알고리즘이다. Q-learning도 동일한데, 이때 한가지 차이가 있다면, SARSA는 현재 policy \(\pi\)에 대한 bellman equation을 sampling된 데이터를 활용해서 푸는 것이었다면, Q-learning은 optimal policy \(\pi_*\)에 대한 bellman equation을 푸는 것이다. 그래서 역시 동일한 update식을 살펴보면 아래와 같다.
$$ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big(\color{red}{R_{t+1}} + \color{red}{\gamma \max_{a'} Q(S_{t+1}, a')} - Q(S_t, A_t) \big) $$
역시 bellman optimality equation도 다음과 같다.
$$ q_{*}(s, a) = \sum_{s', r} p(s', r|s, a) \big(\color{red}{r} + \color{red}{\gamma \max_{a'} q_{\pi}(s', a')} \big) $$
보통 optimal policy라고 하면 현재 policy보다 더 나은 value function을 가지는 policy를 말하게 되는데, 이때문에 주어진 policy에 대한 Q-value를 전부 더하는 것 대신에 Q-value 중에서 가장 큰 값을 얻을 수 있는 것을 취하는 것이 Q-learning의 동작원리이다.
좀 다르게 표현하면 SARSA는 하나의 정해진 policy \(\pi\)를 대상으로 Policy Iteration을 하는 것이고, Q-learning은 Optimal policy \( \pi_* \)를 바탕으로 Value Iteration을 하는 것이다. 이전 포스트에서 잠깐 언급했던 내용 중에 Target policy와 behavior policy간의 일치 유무에 따라 나눠진다고 했었는데, 그 부분이 바로 여기이다.
$$ \begin{align} \text{SARSA : } & Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big(R_{t+1} + \gamma Q(S_{t+1}, \color{red}{A_{t+1}}) - Q(S_t, A_t) \big) \\ \text{Q-learing : } & Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \big(R_{t+1} + \gamma \color{red}{\max_{a'}} Q(S_{t+1}, \color{red}{a'}) - Q(S_{t}, A_{t}) \big) \end{align} $$
SARSA에서 next state-action의 value \(Q(S_{t+1}, A_{t+1})\)를 구하는 필요한 action \(A_{t+1}\)은 현재의 policy \(\pi\)에서 sampling되어 나온 action이다. 반면 Q-learning에서의 next state action을 구하는 부분은 \(a'\)로 표기되어 있는데, 이 action은 optimal policy \(\pi_*\)에서 나온 것이고, 현재 policy \(\pi\)와는 다르다. 이를 강의에서는 다음과 같이 도식화시켰다.
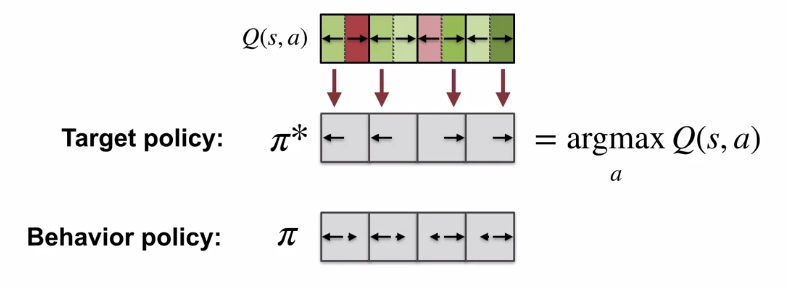
여기서 Behavior policy는 우리가 optimal한 target policy를 찾는 전략을 취할 수 있다. 이를테면 이전에 소개했던 \(\epsilon\)-greedy policy같은 것 말이다. 이를 통해 Q-learning이 off-policy임을 알 수 있다.
그런데 이전 포스트 중 off-policy에 관해서 다뤘던 내용을 본 사람이라면 위의 수식에서 뭔가가 없는 것을 알 수 있을 것이다. 바로 Importance Sampling이다. 잠깐 다시 살펴보면 Target Policy와 Behavior Policy에서 action을 sampling할 때, 이 두 policy간의 distribution 차이를 보정하기 위해서 Importance Sampling을 사용했었다. 그런데 사실 Importance Sampling을 쓰는 이유는 말 그대로 distribution이 다른 action을 보정해주는, 말 그대로 action이 일어날 확률을 보정해주는 것이다. 그런데 앞의 수식을 보면 알겠지만, 우리는 각 action이 일어날 확률을 하나하나 사용하는 것이 아니라, 이중에 가장 큰 Q-value를 주는 action을 선택하는 것이다. 강의에서 소개된 backup diagram을 살펴보면,
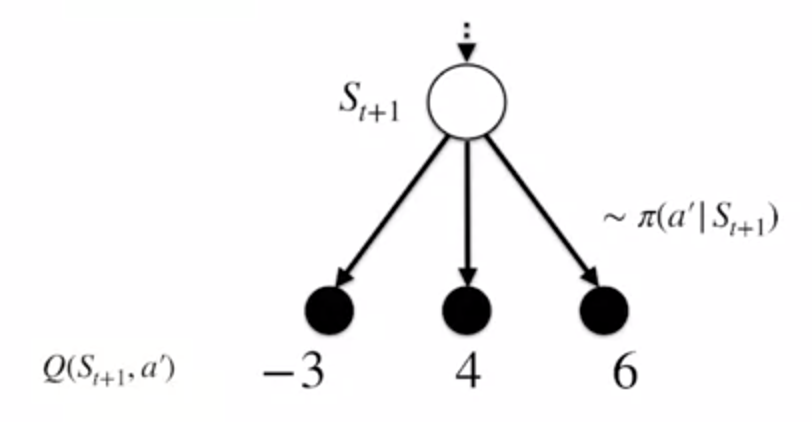
위와 같이 \(S_{t+1}\)에서 action \(a'\)를 취했을 때, 얻을 수 있는 Q-value가 -3, 4, 6이고, 이때의 action은 policy \(\pi(a'|S_{t+1})\)에 따라 결정된다고 가정해본다. 물론 \(S_{t+1}\)에서의 expected return을 구하려면 다음과 같은 수식을 통해서 policy에 Q-value를 곱한 값들을 모두 더했어야 했다.
$$ \sum_{a'} \pi(a'|S_{t+1}) Q(S_{t+1}, a') = \mathbb{E}_{\pi}[G_{t+1}|S_{t+1}] $$
그런데 greedy action을 취하게 되면, 가장 큰 값의 Q-value를 취하는 action을 빼고는 나머지의 action에 대한 probability는 0이 된다. 반대로 가장 큰 값의 Q-value를 얻을 수 있는 action의 probability는 1이 된다.

그렇기 때문에 굳이 Importance sampling을 취하지 않더라도 적절한 action을 선택하고 그렇게 얻은 policy를 target policy로 update시킬 수 있는 것이다.
결국 Q-learning은 앞에서 소개했던 여타 알고리즘과 같이 Policy Iteration을 취하는 것이 아니라 optimal policy를 직접적으로 학습하는 형태를 취한다. 물론 상황에 따라서 달라지겠지만, 책에서 소개되어 있는 Cliff walking 예제를 보면 단점이 조금 보일 수 있다.
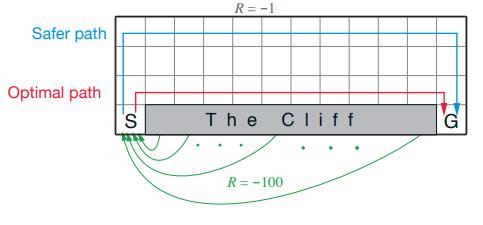
Q-learning같은 경우는 각 action에 대해서 좋은 Q-value를 얻을 수 있는 action을 선택해서 취하기 때문에 좋은 결과를 얻을 수 있지만, 만약 취하는 policy가 \(\epsilon\)-greedy같이 stochastic한 부분이 담겨 있다면, 그만큼 Cliff같은 나쁜 state로 빠질 가능성도 그만큼 높다. 대신 SARSA같은 경우는 전체적인 Q-value를 보고 값을 update하기 때문에 상대적으로 안정적일 가능성이 높다. 실제로 이에 대한 결과를 놓고 봐도 그렇다.

그렇다고 SARSA가 Q-learning보다 더 좋다고 단정지을 수 있는 것은 아니고, 뭔가 Q-learning이 학습이 잘되고, stochastic시 발생할 수 있는 나쁜 부분을 보완할 수 있다면 조금더 좋은 성능을 얻을 수도 있다. 어떤 학습 방법을 취할지는 적용하는 사용자 마음이지 않을까 싶다.
'Study > AI' 카테고리의 다른 글
| [RL] Dyna as a formalism for planning (3) | 2019.09.30 |
|---|---|
| [RL] Model & Planning (0) | 2019.09.25 |
| [RL] Expected SARSA (0) | 2019.09.18 |
| [RL] SARSA : GPI with TD (3) | 2019.09.11 |
| [RL] Introduction to Temporal Difference Learning (2) | 2019.09.06 |
| [RL] Off-policy Learning for Prediction (3) | 2019.09.05 |
| [RL] Exploration Methods for Monte Carlo (0) | 2019.09.04 |
- Total
- Today
- Yesterday
- Off-policy
- SketchFlow
- PowerPoint
- Distribution
- 한빛미디어
- ColorStream
- Kinect for windows
- dynamic programming
- Pipeline
- arduino
- processing
- windows 8
- Gan
- 인공지능
- Windows Phone 7
- 딥러닝
- 파이썬
- Kinect
- Expression Blend 4
- Offline RL
- RL
- TensorFlow Lite
- Kinect SDK
- reward
- End-To-End
- Policy Gradient
- bias
- Variance
- DepthStream
- 강화학습
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
