티스토리 뷰
(해당 포스트는 Coursera의 Prediction and Control with Function Approximation의 강의 요약본입니다)
이전 포스트를 통해서 기존의 tabular method가 아닌 Function Approximation으로 value function을 정의하는 방법을 대략적으로 설명했다. 일단 뭐가 되던 간에 우리가 만들 value function은 각 state에 대한 value function이 차별성을 잘 띄고 있어야 하고(high discrimination), 전체 state에 대한 일반화도 잘되어야 한다.(high generalization)
그렇게 해서 어떤 linear value function \( \hat{v}(s, \mathbf{w})\) 을 만들었다고 가정해보자.
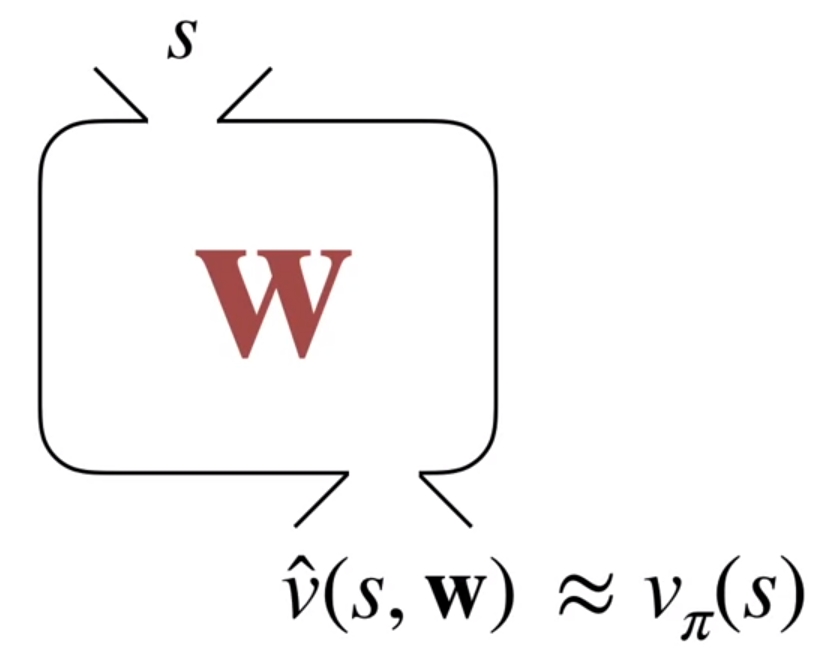
그러면 이렇게 근사된 value function이 잘 만들어졌는지를 판단하는 기준이 있어야 한다. 일단 잘 근사가 되었다면 실제의 value function \(v_{\pi}(s)\)와 거의 동일하거나 오차가 적어야 한다. 물론 function approximation이 처음부터 잘되지는 않을 것이고, 몇몇 iteration이 진행되면서 weight \(\mathbf{w}\) 이 실제 value function과의 오차가 적어지는 방향으로 수정되는게 이상적인 과정이 될 것이다. 이때 이 근사화된 value function과 실제의 value function간의 오차를 정의한 식을 Value Error(VE) Objective라고 하고, 책이나 수식에서는 \(\overline{VE}\)로 표기한다. 여기서 둘간의 Mean Squared Error를 계산한다.
$$ \overline{VE} \approx \sum_{s \in S} [v_{\pi}(s) - \hat{v}(s, \mathbf{w})]^2 $$
그런데 위 식에서 Error를 계산할 때 왜 근사치로 표기했는지 의문을 가질 수 있는데, 아래의 그래프를 잠깐 살펴보면 위 식이외도 별도의 항이 필요하다는 것을 알게 된다.
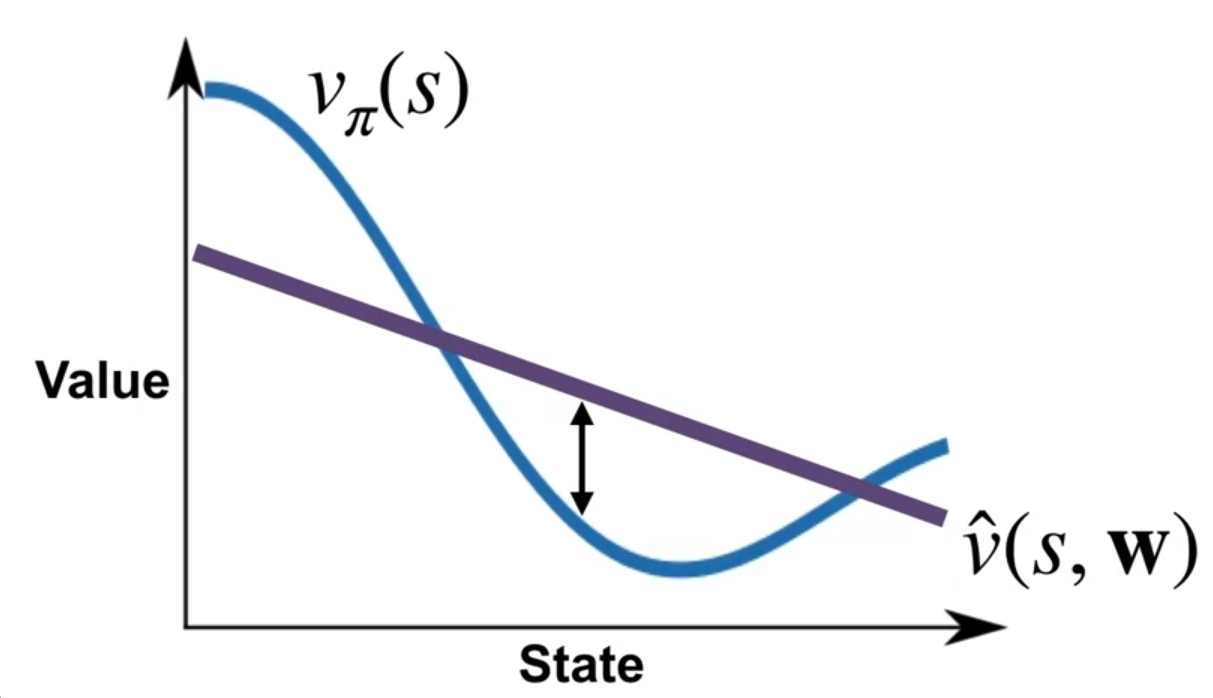
위 그림에서 파란색 선이 실제의 value function이고, 보라색 선이 근사화된 value function이 되고, 앞에서 언급한 대로라면 Value Error는 두 선 사이의 거리의 제곱으로 계산할 수 있다. 문제는 실제의 value function은 다차항이고, 근사된 value function이 단항이라면, 아무리 weight를 수정한다고 해도 Value Error가 작아지지 않는다는 것이다. 생각해보면 weight를 수정해서 특정 state에서의 Value Error가 작아졌다 할지라도 다른 state에서의 Value Error는 커질 수도 있다. 이 때문에 각 state별로 뭔가의 가중치를 더해서 각각 중요성을 구분짓게 하는 것이 필요하다. 그래서 진짜 Value Error Objective에서는 이 state별 가중치를 표시한 \(\mu(s)\)라는 것이 추가되고, 식으로는 다음과 같이 표기 된다.
$$ \overline{VE} \doteq \sum_{s \in S} \mu(s) \big[ v_{\pi}(s) - \hat{v}(s, \mathbf{w})\big]^2 $$
이를 통해서 value error를 구할 때마다 해당 값이 전체 objective function에 영향을 끼칠지를 \(\mu(s)\)를 통해서 정할 수 있다. 여기서 \(\mu(s)\)는 현재의 policy \(\pi\)상에서 \(S\)내의 각 state \(s\)에 방문한 횟수를 비율로 표현한 것이다. 다시 말해 현재 policy에서 특정 state에 많이 방문했다는 것은 그만큼 그때의 value function이 value function approximation에 영향을 많이 끼친다는 것이고, 그만큼 \(\mu(s)\)도 클 것이다. 당연히 거기서 error를 minimize하면 그만큼 근사된 value function이 실제 value function과 유사하게 된다.
아마 이렇게 Error objective가 나왔으니까, 많이들 아는 Gradient Descent를 통해서 이 Error를 Minimize하도록 학습을 시킬 수 있게 된다. 일단 weight에 대한 Value error objective가 아래와 같다고 가정해보자.
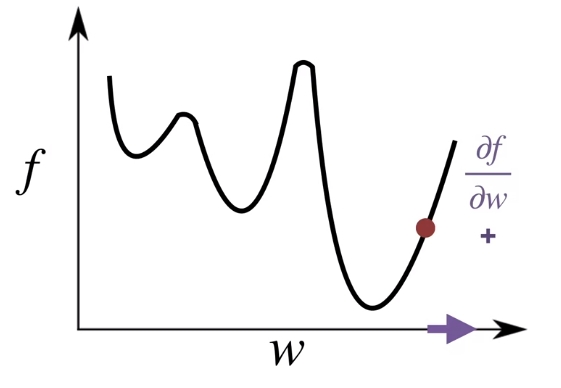
Value Error Objective의 목표는 말그대로 Value Error를 찾는데 있다. 위의 그래프로 따지면 가장 낮은 값을 찾아야 하는데, 이때 함수의 gradient를 이용한다. 일반적으로 이 gradient는 \(w\)가 변함에 따라서 \(f\)가 증가하는지 감소하는지를 부호를 통해서 알려준다. 그리고 gradient의 magnitude는 \(w\)의 변화에 따라서 \(f\)가 얼마나 변하는지 그 변화 정도를 나타낸다.
그런데 갑자기 함수를 weight로 미분하고 복잡하게 느낄 수 있다. 하지만 우리가 원하는 것은 각 weight에 대한 partial derivative이므로 weight을 vector form으로 생각해보면 미분값은 간단하게 생각할 수 있다. 우선 state가 \(d\)개 있을 때, 이에 대한 weight\(w\)과 objective function \(f\)에 대한 각각의 partial derivative는 다음과 같다.
$$ w \doteq \begin{bmatrix} w_1 \\ w_2 \\ \dots \\ w_d \end{bmatrix} \nabla f \doteq \begin{bmatrix} \frac{\partial f}{\partial w_1} \\ \frac{\partial f}{\partial w_2} \\ \dots \\ \frac{\partial f}{\partial w_d} \end{bmatrix} $$
그러면 partial derivative의 결과는 objective function \(f\)가 변화하는데 있어, weight \(w_d\)가 변화하는 방향과 얼마나 빨리 변하는지를 나타낸 것이 된다. 이때 objective function내 \(w_d\)가 포함되지 않은 항은 상수를 미분하는 꼴이 되므로 미분시 0으로 된다. 그러면 앞에서 한 가정 그대로 objective function을 function approximation으로 얻은 Linear value function이라고 해보자 그러면 해당 value function을 각 weight로 partial derivative를 하게 되면 결국 해당 state 값만 남게 된다.
$$ \begin{align} \hat{v}(s, \mathbf{w}) & \doteq \sum w_i x_i(s) \\
\frac{\partial \hat{v}(s, \mathbf{w})}{\partial w_i} &= x_i(s) \\ \end{align}$$
그러면 vector 연산식으로 나타낸 Value function의 gradient는 결국 각 state 그대로라는 것으로 정리해볼 수 있다.
$$ \nabla \hat{v}(s, \mathbf{w}) = \mathbf{x}(s) $$
그러면 아래와 같이 value error objective가 있다고 가정해보자.
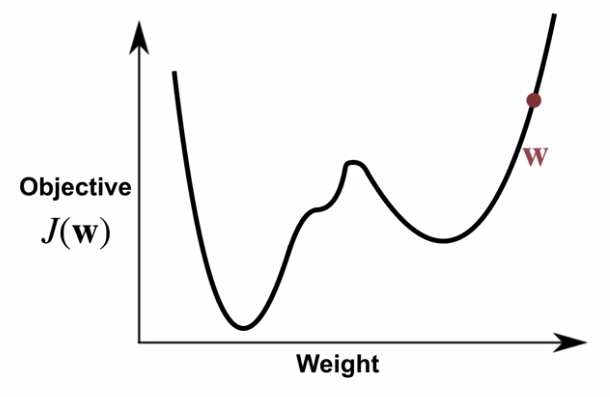
이 값은 실제 값과 예측값에 대한 mean-squared error이므로 우리가 원하는 것은 이 error가 가장 작아지는 weight을 찾는 것이다. 한마디로 전체 함수의 최소값 (Global minimum)을 찾아야 된다. 여기서 우리가 임의로 시작한 weight이 \(\color{red}{\mathbf{w}}\)라면, Global minimum을 나타내는 weight \(\mathbf{w}_*\)를 찾기 위해서는 weight을 감소하는 방향으로 update해줘야 한다. 보통 update할 때는 한번 update할 때 얼마만큼 변화를 줄건지 결정하는 step size parameter \(\alpha\)를 정의하곤 한다.
$$ \mathbf{w}_{t+1} \doteq \mathbf{w}_t - \alpha \nabla J(\mathbf{w}_t) $$
만약 이렇게 gradient descent로 weight를 update하다보면 gradient가 0인 지점으로 결국 수렴하게 되는데, 위와 같이 convex가 2개인 경우에는 내가 찾은 값이 최소점이 아닌 그냥 gradient만 0인 극소점(local minimum)에 도달하는 경우도 발생할 수 있다.
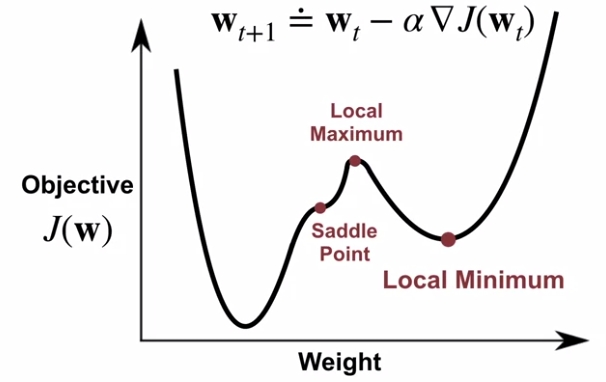
이밖에도 내가 찾은 값이 극대값 (Local Maximum)이나 안장점 (Saddle point - 말의 안장처럼 생겼다고 해서 saddle point란다..) 이 될 수도 있어서 어떤 step size와 어떤 update 함수를 가지는지에 따라서 결과가 달라지게 된다. 일반적으로 앞에서 소개한 Linear Function Approximation 같은 경우는 gradient descent를 사용하면 global minimum을 찾게되고, Neural Network을 사용한 Complex Function Approximation 같은 경우는 Global minimum을 못 찾을 가능성이 존재한다.
그럼 이런 gradient descent를 앞에서 구했던 value error objective에서 적용해보면 다음과 같이 전개해볼 수 있다.
$$ \begin{align} \nabla \color{red}{\sum_{s \in S} \mu(s)} \big[ v_{\pi}(s) - \hat{v}(s, \mathbf{w})\big]^2 &= \color{red}{\sum_{s \in S} \mu(s)} \nabla \big[ v_{\pi}(s) - \hat{v}(s, \mathbf{w})\big]^2 \\ &= - \color{red}{\sum_{s \in S} \mu(s)} 2 \big[ v_{\pi}(s) - \hat{v}(s, \mathbf{w}) \big] \nabla \hat{v}(s, \mathbf{w}) \end{align} $$
만약 우리가 Linear function Approximation을 사용했다면,
$$ \hat{v}(s, \mathbf{w}) \doteq < \mathbf{w}, \mathbf{x}(s) > $$
와 같이 inner product의 형태가 될 것이고, 각 weight에 대한 gradient를 취하면 앞에서 언급한 것처럼 feature vector만 남게 될 것이다.
$$ \nabla \hat{v}(s, \mathbf{w}) = \mathbf{x}(s) $$
결국 우리가 알 수 있는 것은 실제의 value function \(v_{\pi}(s)\)와 estimate된 value function \(\hat{v}(s, \mathbf{w})\)간의 error가 결국 weight과 비례하다는 것이다.
$$ \Delta \mathbf{w} \propto \color{red}{\sum_{s \in S} \mu(s)} \big[ v_{\pi}(s) - \hat{v}(s, \mathbf{w}) \big] \nabla \hat{v}(s, \mathbf{w}) $$
예를 들어서 value function 들간의 error가 작으면 작을수록 weight의 변화도 작아질 것이고, 이 error의 변화가 weight의 변화에 영향을 끼친다는 것이다.
사실 위에 나온 이야기만 가지고 본다면, Gradient descent만 쓰면, value error objective에서도 error가 적어지는 방향으로 weight이 수정될 것이고, 이를 통해서 정확한 value function을 근사할 수 있을거라는 생각이 든다. 하지만 앞의 식들에서 살짝 나와있는 것처럼 weight의 gradient를 구하기 위해서는 이 부분이 해결되어야 한다.
$$ \color{red}{\sum_{s \in S} \mu(s)} $$
즉, 모든 state에서의 가중치를 모두 더한 값을 알아야 하는데, 이게 계산하는데 있어 그렇게 좋은 방법이 아니다. 대신 실제 현재의 policy \(\pi\)의 value function을 직접 수행하면서 얻은 샘플값을 가지고 정확한 값은 아니더라도 대충 어떤 값을 가지겠다 정도의 근사값을 구할 수 있다.
일단 아래와 같이 State, value tuple이 있다고 가정해보자.
$$ (S_1, v_{\pi}(S_1)), (S_2, v_{\pi}(S_2)), (S_3, v_{\pi}(S_3)), \dots $$
이때 다음 weight \(\mathbf{w}_2\)는 위에 나온 식을 활용해서 다음과 같이 구할 수 있다.
$$ \mathbf{w}_2 \doteq \mathbf{w}_1 + \alpha [v_{\pi}(S_1) - \hat{v}(S_1, \mathbf{w}_1)] \nabla \hat{v}(S_1, \mathbf{w}_1) $$
이렇게 하면 \(S_1\)에서의 value error가 적어지는 방향으로 \(\mathbf{w}_2\)가 update될 것이고, 동일한 방식으로 따라가면 각 state에서의 value error가 적어지는 방향으로 weight들이 update될 것이다. 앞에서 소개한 방식과 차이라면, 앞의 방식은 전체 state에 대한 value error를 알고있는 상태에서 weight이 update되는 정도를 결정할 수 있는데, 지금 소개한 방식은 굳이 전체 state를 몰라도 현재 state의 value error만 가지고도 다음 state에서의 value error를 줄일 수 있다는 것이다. 이러한 전개는 현재의 policy \(\pi\)가 동작하는 상황에서라면 궁극적으로 value error가 적어지는 방향으로 동작된다. 이런 방식을 Stochastic Gradient Descent (SGD)라고 표현한다. 다르게는 batch size가 1인 gradient descent라고 말하기도 한다.
이렇게 구한 결과는 사실 일반 gradient descent에 비하면 약간 오차가 발생할 수 있지만, 실제로 필요한 연산량을 고려해보면 훨씬 효율적이기 때문에 Stochastic Gradient Descent를 많이 활용하곤 한다. 그런데 문제는 우리가 과연 value function에 대한 ground truth (\(v_{\pi}(s)\))를 알고있냐는 것이다. 지금 앞에서 소개한 방법들이 다 Value function에 대한 approximation을 하자는 것이고, 이를 위해서 error가 최소화되는 방향으로 gradient descent를 취해야 하는데 error를 구할 실제 value function을 우리가 모르고 있다는 것이다. 여기서 이전 Monte Carlo Method에서 언급했던 내용중 하나인 value function의 정의를 다시 가져올 수 있다. 그때 특정 state에 대한 value function을 다음과 같이 기술할 수 있었다.
$$ v_{\pi}(s) \doteq \mathbb{E}_{\pi} [ G_t | S_t = s ] $$
이 특징을 활용하면 weight에 대한 update때도 \(v_{\pi}(s)\)가 아닌 \(G_t\)를 활용할 수 있고,
$$ \begin{align} \mathbf{w}_{t+1} & \doteq \mathbf{w}_t + \alpha [v_{\pi}(S_t) - \hat{v}(S_t, \mathbf{w}_t)] \nabla \hat{v}(S_t, \mathbf{w}_t) \\ & \doteq \mathbf{w}_t + \alpha [G_t - \hat{v}(S_t, \mathbf{w}_t)] \nabla \hat{v}(S_t, \mathbf{w}_t) \end{align} $$
당연히 gradient에 대한 expectation도 동일하게 \(G_t\)를 사용할 수 있다.
$$ \mathbb{E}_{\pi} \big[ 2 [ v_{\pi}(S_t) - \hat{v}(S_t, \mathbf{w})] \nabla \hat{v}(S_t, \mathbf{w} \big] = \mathbb{E}_{\pi} \big[ 2 [ G_t - \hat{v}(S_t, \mathbf{w})] \nabla \hat{v}(S_t, \mathbf{w} \big] $$
이 식을 정리한 것이 Gradient Monte Carlo Algorithm이고, 책에서는 다음과 같이 정의되어 있다.

간단히 설명하자면, \(\hat{v}\)를 \(v_{\pi}\) 로 근사하기 위해서 (엄밀히 말하자면 둘간의 error를 줄이기 위해서) Monte Carlo가 가지고 있는 특성중 하나인 \(G_t\)를 사용했다는 것이다.
여기에 하나 생각해볼 수 있는 것이 Value function approximation을 할 때 조금더 빠르게 효율적으로 해볼 수 있지 않을까 이다. 사실 Monte Carlo method의 특성상 episode가 끝나야 계산될 수 있고, 만약 epsiode내 방문한 state의 갯수가 많다던가, environment 자체가 가진 state가 많다면 그만큼 value function을 구하는데 시간이 많이 들 것이다. 이때 적용해볼 수 있는 것이 State Aggregation이라는 것이다. Aggregation이란 단어가 "집합"이란 뜻을 가지고 있는데, 말그대로 여러개의 state를 하나의 group으로 구분지어서 value function를 고려해보자는 것이다. 예를 들어서 1~1000까지의 state가 있으면 Ground Truth에 해당하는 value function은 1000개 state 모두에 대한 value가 정의되어 있어야 하지만, 만약 1~100을 1 그룹, 101-200을 2 그룹, ... 이런식으로 100개씩 그룹을 짓게 되면 10개의 value에 대해서만 정의하면 된다. 물론 1000개를 모두 고려했을 때의 value function을 구할 수는 없겠지만, 아무래도 우리의 목적이 policy improve를 하는 것이지, value function을 정밀하게 estimate하는 것이 아니기 때문에, 그만큼 state를 줄이는 것이 도움이 될 수 있다. 어차피 value function approximation에 사용되는 state 방문에 대한 빈도를 나타내는 \(\mu(s)\)를 하나하나로 볼것이냐, 아니면 group을 나눠서 볼것인가의 영향이 달라지는 것일뿐 Value Function approximation으로 구한 결과나 실제 결과나 큰 차이가 없다.
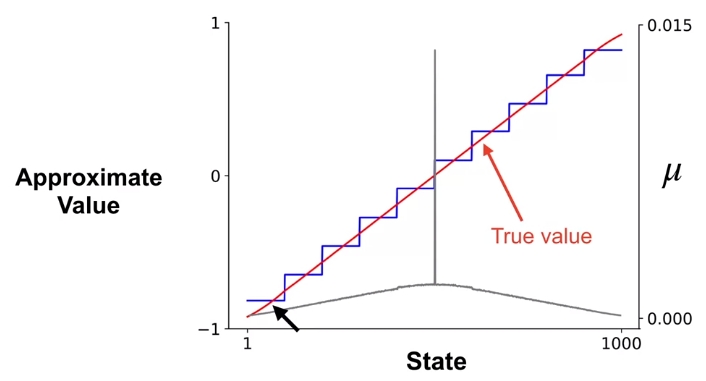
지금까지 Value function approximation을 하는데 있어, 실제값과 approximate된 값간의 차이를 나타내는 Value Error Objective가 필요하다는 것과 이를 On-policy Monte Carlo에 적용한 케이스인 Gradient Monte Carlo, 마지막으로 Value Function Approximation시 발생할 computation efficiency를 위한 State Aggregation 방법에 대해서 다뤄봤다.
'Study > AI' 카테고리의 다른 글
| [RL] Meta Reinforcement Learning (2) | 2019.11.14 |
|---|---|
| [RL] Linear TD (0) | 2019.11.12 |
| [RL] The Objective of TD (0) | 2019.11.12 |
| [RL] Estimating value function with supervised learning (0) | 2019.11.06 |
| [RL] Dealing with inaccurate models (0) | 2019.10.08 |
| [RL] Dyna as a formalism for planning (3) | 2019.09.30 |
| [RL] Model & Planning (0) | 2019.09.25 |
- Total
- Today
- Yesterday
- arduino
- ColorStream
- windows 8
- Off-policy
- PowerPoint
- TensorFlow Lite
- RL
- Kinect
- 인공지능
- DepthStream
- 강화학습
- reward
- Offline RL
- Policy Gradient
- processing
- 딥러닝
- bias
- Pipeline
- End-To-End
- Expression Blend 4
- Kinect for windows
- 한빛미디어
- SketchFlow
- dynamic programming
- Distribution
- Kinect SDK
- 파이썬
- Gan
- Variance
- Windows Phone 7
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
