티스토리 뷰
(해당 글은 OpenAI Engineer인 Lilian Weng의 포스트 내용을 원저자 동의하에 번역한 내용입니다.)
Meta Reinforcement Learning
Meta-RL is meta-learning on reinforcement learning tasks. After trained over a distribution of tasks, the agent is able to solve a new task by developing a new RL algorithm with its internal activity dynamics. This post starts with the origin of meta-RL an
lilianweng.github.io
Meta-RL은 강화학습 task에 meta learning을 적용한 것이다. 여러 가지로 분포된 task를 학습한 agent는 내부적으로 이뤄지는 activity에 대한 dynamics를 통해서 새로운 강화학습 알고리즘을 개발함으로써 새로운 task를 해결할 수 있게 된다. 이 포스트에서는 meta-RL의 기원에서 출발해서, meta-RL을 구성하는 3가지 핵심요소를 다뤄보고자 한다.
meta-learning에 대해서 다룬 이전 포스트(번역)에서, 문제는 주로 few-shot classification내에 정의되어 있었다. 여기서는 경험하지 못한 task에 대해서 빠르고 효율적으로 해결할 수 있는 agent를 개발함으로써 "meta-learn" 강화학습 task를 해결하는 경우에 대해서 조금더 다뤄보고자 한다.
meta-learning에 대해서 다시 다뤄보자면, 좋은 meta-learning 모델은 training 단계에서 전혀 경험하지 못했던 새로운 task나 environment에 대해서도 generalize할 수 있는 성능을 보여주는 것으로 기대된다. adaptation 과정, 엄밀히 말하자면 mini learning session 단계는 새로운 설정에 제한적으로 노출되는 test 과정에서 이뤄진다. (어떠한 gradient backpropagation이나 trainable한 변수가 없는) 특별한 fine-tuning 과정없이도, meta-learning 모델은 자동적으로 학습을 통해 내부의 숨겨진 state에 대해서 적응한다.
사실 강화학습 알고리즘을 학습하는 것은 때때로 어려울 수 있다. 만약 meta-learning agent가 경험하지 못했지만 해결할 수 있는 task들의 범위가 매우 넓어질 만큼 매우 똑똑해진다면, 널리 알려진 방법을 사용해볼 수 있는데, 이건 본질적으로 인간의 관여나 일일이 feature engineering 하는 것 없이도 모든 종류의 강화학습 문제를 해결할 수 있는 "brain"을 만들자는 것이다. 듣기만 해도 굉장하지 않을까?
On the Origin of Meta-RL
Back in 2001
Wang et al, 2016을 읽을 때, 2001년에 쓰여진 Hochreiter et al, 2001 도 찾아보게 되었다. 여기에 소개된 아이디어는 supervised learning에 관한 것이지만, 여기에는 현재의 방법들을 meta-RL에 접목시킬 수 있는 접점들이 많이 있었다.

Hochreiter가 제안한 meta-learning 모델은 LSTM cell로 이뤄진 recurrent network이다. LSTM은 input에 대한 history를 내장하면서, 그것들에 대한 각각의 weight을 BackPropagation Through Time(BPTT)을 통해서 효율적으로 조절할 수 있기 때문에 좋은 선택이 된다. training data는 \(K\)개의 sequence를 가지고, 각 sequence는 target function \(f_k(\dot), k=1, \dots, K\)에 의해서 생성된 \(N\)개의 sample들로 구성되어 있다.
$$ \{\text{input: }(\mathbf{x}^k_i, \mathbf{y}^k_{i-1}) \to \text{label: }\mathbf{y}^k_i\}_{i=1}^N
\text{ where }\mathbf{y}^k_i = f_k(\mathbf{x}^k_i) $$
위 식에서 가장 최근의 label인 \(y_{i-1}^k\)도 보조 input으로 제공해줘서 target function이 현재의 mapping 관계를 학습할 수 있도록 해준다. \(a x_1^2 + b x_2^2 + c x_1 x_2 + d x_1 + e x_2 + f\)와 같이 각 계수 \(a-f\)가 \([-1,1]\)사이에서 random하게 sampling되는 2차 이항 방정식으로 해결해야하는 문제에서 위에 소개된 meta-learning system은 35개 미만의 샘플만 보고서도 함수를 approximate할 수 있었다.
Proposal in 2016
딥러닝이 활발히 개발되는 시점에, Wang et al, 2016 과 Duan et al, 2017은 거의 동시에 Meta-RL에 대해서 비슷한 아이디어를 내놨다. (두번째 논문은 보통 \(\text{RL}^2\)라고 부르기도 한다.) meta-RL 모델은 다양한 MDP에 대해서 학습하고, test 시점에서는 새로운 task를 빠르게 해결할 수 있게끔 학습한다. meta-RL의 목표는 일반적인 알고리즘을 한단계 넘어서는 의욕적인 것이었다.
Define Meta-RL
Meta Reinforcement Learning은 간단하게 말해서, reinforcement learning 범주 내에서 meta-learning을 적용하는 것이다. 일반적으로 train task와 test task가 다르지만, 같은 범주의 문제에서 다뤄진다. 예를 들어서 논문에서는 서로 다른 reward probability를 가지는 multi-armed bandit 문제나, 다른 구조의 미로, 시뮬레이터에서 서로 다른 physical parameter를 가진 로봇 같은 것들이 이런 특성을 가지고 있다.
Formulation
예를 들어, 각각 MDP (Markov Decision Process)로 구성된 \(M_i \in \mathcal{M}\) 다양한 task들이 있다고 해보자. 보통 MDP는 4개의 요소로 이뤄진 tuple로 되어 있다. (\(M_i= \langle \mathcal{S}, \mathcal{A}, P_i, R_i \rangle \)) :
| Symbol | Meaning |
| \(\mathcal{S}\) | State의 집합 |
| \(\mathcal{A}\) | Action의 집합 |
| \(P_i: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \to \mathbb{R}_{+}\) | Transition Propability function |
| \(P_i: \mathcal{S} \times \mathcal{A} \to \mathbb{R} \) | Reward function |
(\(\text{RL}^2\) 논문에서는 각 MDP가 finite horizon을 가지는 것을 강조하기 위해서, horizon \(T\)라는 별도의 parameter가 MDP tuple 내에 포함되어 있다.)
유념할 것은 위에 소개된 state \(\mathcal{S}\)과 action space \(\mathcal{A}\)을 사용했을 때, (stochastic) policy (\(\pi_{\theta} : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}_{+}\)는 서로 다른 task에 맞게끔 input을 넣게 된다. 이때 test task는 \(\mathcal{M}\)의 분포를 가지거나 여기서 약간 수정된 형태에서 sampling된다.

Main Difference from RL
meta-RL의 전체적인 설정은 일반적인 RL 알고리즘과 매우 유사한데, 한가지 차이가 있다면 가장 마지막 reward \(r_{t-1}\)과 action \(a_{t-1}\) 또한 현재의 state \(s_t\)에 추가되어 policy observation에 사용된다는 것이다.
- RL : \(\pi_{\theta}(s_t) \rightarrow \mathcal{A}\)에 대한 분포
- meta-RL : \(pi_{\theta}(a_{t-1}, r_{t-1}, s_t) \rightarrow \mathcal{A} \)에 대한 분포
이렇게 설계한 의도는 model에게 과거 내역을 전달해서, policy가 현재 MDP에 대한 state, action reward들간의 dynamics를 내제화하고, 이에 따라 전략을 수정할 수 있게끔 하자는 것이었다. 이런 구조는 앞에서 소개한 Hochireiter 논문에서 소개된 system의 구성과 일맥상통한다. meta-RL과 \(\text{RL}^2\) 모두 LSTM policy가 구현되어 있고, LSTM의 hiddent state는 trajectory들의 특성을 추적하기 위한 일종의 memory 역할을 수행한다. 이 경우 policy가 recurrent하기 때문에, 명시적으로 마지막 state를 입력으로 넣어줄 필요가 없게 된다.
training process는 다음과 같이 동작한다.
- 새로운 MDP (\(\mathcal{M}_i \sim \mathcal{M} \))을 sampling한다.
- model이 가지고 있는 hidden state를 초기화한다.
- 이후 여러개의 trajectory를 얻고, 이를 바탕으로 model의 weight를 update한다.
- 1번 과정으로 돌아가 다시 수행한다.
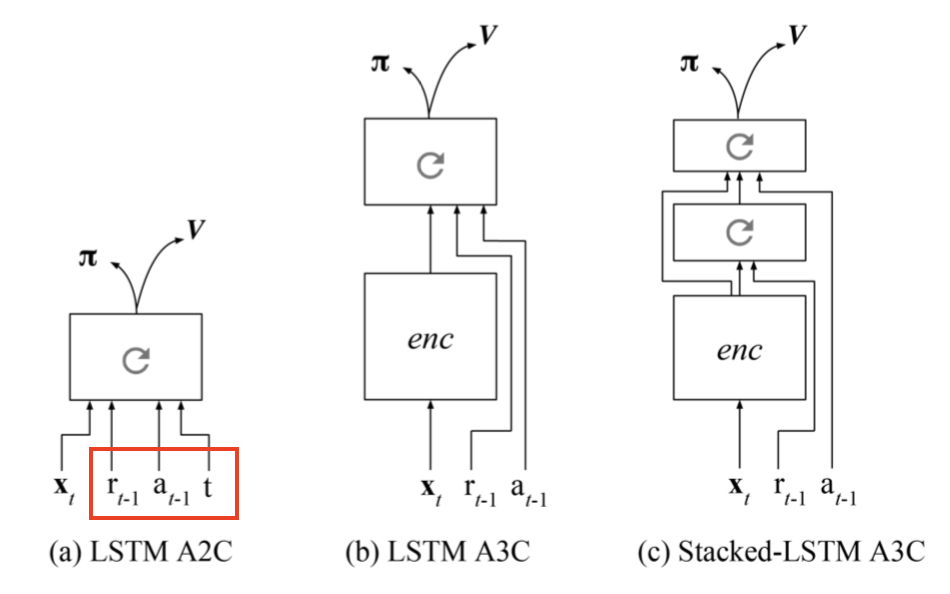
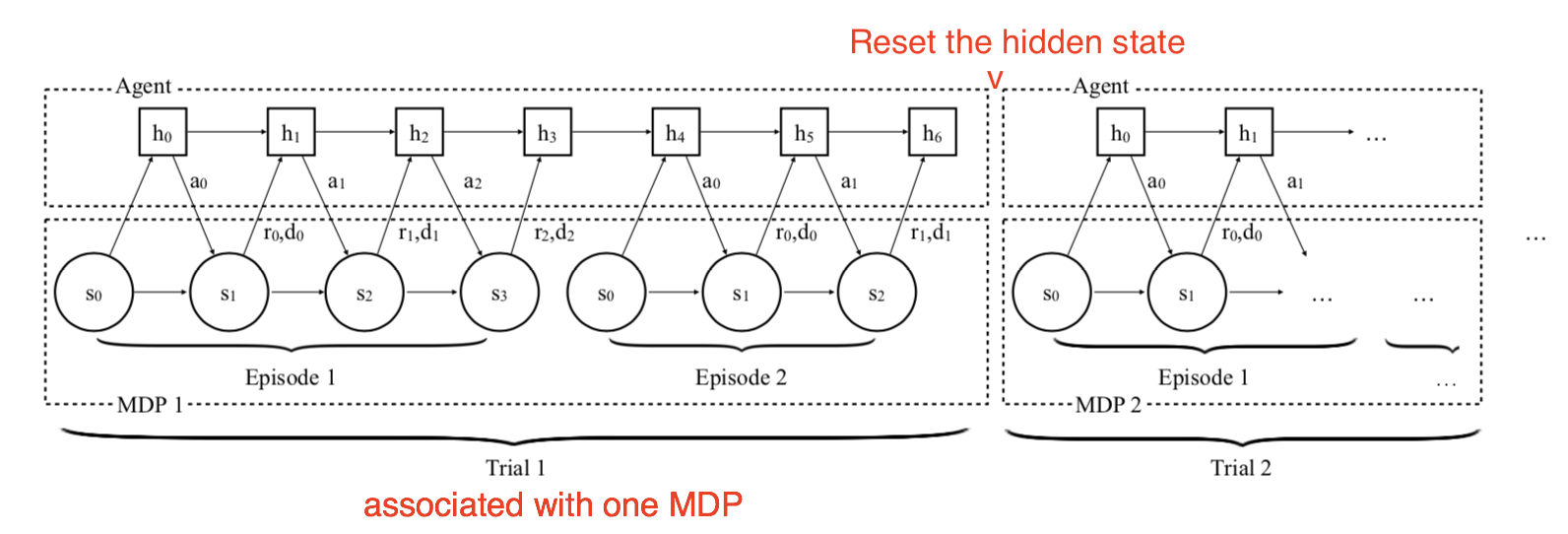
Key Components
Meta-RL을 구성하는 3가지 요소는 다음과 같다:
* Memory를 가지는 Model
recurrent neural network은 hidden state를 항상 유지하고 있다. 그렇기 때문에 rollout등을 통해서 hidden state를 update함으로써, 현재의 task에 대한 지식을 쌓고 기억할 수 있게된다. Memory가 없으면 meta-RL은 동작하지 않는다.
* Meta-learning 알고리즘
meta-learning 알고리즘은 test 시점에 경험하지 못한 task를 빠르게 해결하는 목적으로 model의 weight를 어떻게 update하느냐에 달려있다. meta-RL 논문이나 \(\text{RL}^2\) 논문에서는 모두 meta-learning 알고리즘을 MDP들이 전환되는 동안 hidden state가 초기화되는 LSTM에다가 일반적인 gradient descent를 통해서 update하는 방식을 취한다.
* 다양한 MDP
agent가 training동안 다양한 환경과 task에 대해서 노출되는 동안, 서로 다른 MDP에 대해서 적응을 어떻게 할 것인가를 학습해야 한다.
Botvinick et al, 2019 논문에 따르면, RL training에 있어서 학습이 느리게 되는 요인 중 하나가 weak inductive bias (즉, 이전에 주어지지 않았던 input이 새롭게 주어졌을때, output을 예측하기 위해 사용되는 일종의 가정법들) 이다. 일반적인 ML 원칙에 따르면 weak inductive bias를 가진 학습 알고리즘은 다양한 범주의 분산에 대해서 학습할 수 있게되지만, 종종은 sample-efficiency가 떨어지는 경향이 있다. 그렇기 때문에 stronger inductive bias를 통해서 가진 hypothesis 간의 간격을 줄이는 것은 학습 속도를 높이는데 도움이 된다.
meta-RL에서는 task distribution으로부터 어떤 형태의 inductive bias를 새로 도입하고, 그것들을 memory에 저장한다. 어떤 inductive bias가 test 시간에 적용될지는 알고리즘에 따라서 달라진다. 이와 함께, 위의 3개의 요소들은 meta-RL에 대한 전반적인 형태를 묘사한다: recurrent network의 weight을 변화시키는 것은 느리기는 하지만 model이 스스로 가지고 있는 activity dynamics내의 RL 알고리즘을 통해서 새 task에 대해서 빠르게 동작할 수 있게끔 해준다.
Meta-RL은 놀랍지 않게도 Jeff Clune, 2019 논문에서 소개된 AI-GAs("AI-Generating Algorithms")의 아이디어와 일치한다. 그는 general AI를 만드는 방법 중 효율적인 방법으로 학습을 가능한한 자동적으로 하게 하는 것을 제안했다. AI-GA 방식은 3가지 형태를 갖추고 있는데, 첫째는 meta-learning architecture, 둘째는 meta-learning 알고리즘, 셋째는 효율적인 학습을 위해서 environment를 자동적으로 생성하는 것이었다.
좋은 recurrent network을 만드는 것에 대한 내용은 여기서 다루기에는 너무 광범위하기 때문에 넘어가고자 한다. 다음으로 나머지 두가지 요소인 meta-RL에서 쓰이는 meta-learning 알고리즘과 다양한 학습 MDP를 어떻게 얻는지에 대해서 다뤄보고자 한다.
Meta-Learning Algorithms for Meta-RL
Optimizing Model Weights for Meta-Learning
MAML (Finn et al, 2017)이나 Reptile (Nichol et al, 2018) 모두 새로운 task에 대해서 좋은 generalization 성능을 얻기 위해서 model parameter를 update하는 방법에 대해서 다뤘다.
Meta-learning Hyperparameters
\(G_t^{(n)}\)이나 \(G_t^{\lambda}\)로 표현되는 RL 문제의 return function은 discount factor인 \(\gamma\)나 bootstrapping parameter인 \(\lambda\)와 같이 heuristic하게 설정되어 있는 몇몇 hyperparameter들과 연계되어 있다. Meta-gradient RL (Xu et al, 2018) 에서는 이 값들을 \(\eta = \{\gamma, \lambda\}\)라고 하는 meta-parameter로 표현했다. 그래서 agent가 environment와 interaction이 발생하는 동안 online으로 tuning되고 학습할 수 있다고 했다. 결과적으로 return function은 \(\eta\)에 관한 함수가 되며, 시간내 특정 task에 대해서 유동적으로 값이 수정된다.
$$ \begin{aligned}
G_\eta^{(n)}(\tau_t) &= R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{n-1}R_{t+n} + \gamma^n v_\theta(s_{t+n}) & \scriptstyle{\text{; n-step return}} \\
G_\eta^{\lambda}(\tau_t) &= (1-\lambda) \sum_{n=1}^\infty \lambda^{n-1} G_\eta^{(n)} & \scriptstyle{\text{; λ-return, mixture of n-step returns}}
\end{aligned} $$
training동안에는 보통 모든 정보들이 다 담겨져 있는 하나의 함수로써 policy parameter와 이에 대한 gradient를 update하고 싶을텐데, 여기서는 \(\theta' = \theta + f(\tau, \theta, \eta)\)로 표현하고 여기서 \(theta\)는 현재 model의 weight, \(\tau\)는 trajectory들에 대한 과거 정보들, 그리고 \(\eta\)는 meta-parameter를 나타낸다.
반면, 이에 대한 성능을 측정할 수 있는 \(J(\tau, \theta, \eta)\)라는 meta-objective function이 있다고 해보자. 이때 training process는 이전에 쌓았던 consecutive experience를 가지고 online cross-validation의 원칙을 따르게 된다.
- Parameter \(\theta\)에서 시작해서, policy \(\pi_{\theta}\)는 첫번째 batch sample인 \(\tau\)에 대해서 update하고 이 결과를 \(\theta'\)에 넣는다.
- 그 후에 새로운 experience인 \(\tau'\)를 얻기 위해서 policy \(\pi_{\theta'}\)를 계속 수행하고, 이걸 이전에 얻었던 \(\tau\)에 이어서 기록한다. 이 때의 성능은 정해진 meta parameter인 \(\bar{\eta}\)를 가지는 \(J(\tau', \theta', \bar{\eta})\)로 측정한다.
- Meta-objective \(J(\tau', \theta', \bar{\eta})\)를 \(\eta\) 대한 gradient를 취해서 이를 \(\eta\)를 update하는데 활용한다.
$$\begin{aligned}
\Delta \eta
&= -\beta \frac{\partial J(\tau', \theta', \bar{\eta})}{\partial \eta} \\
&= -\beta \frac{\partial J(\tau', \theta', \bar{\eta})}{\partial \theta'} \frac{d\theta'}{d\eta} & \scriptstyle{\text{ ; single variable chain rule.}} \\
&= -\beta \frac{\partial J(\tau', \theta', \bar{\eta})}{\partial \theta'} \frac{\partial (\theta + f(\tau, \theta, \eta))}{\partial\eta} \\
&= -\beta \frac{\partial J(\tau', \theta', \bar{\eta})}{\partial \theta'} \Big(\frac{d\theta}{d\eta} + \frac{\partial f(\tau, \theta, \eta)}{\partial\theta}\frac{d\theta}{d\eta} + \frac{\partial f(\tau, \theta, \eta)}{\partial\eta}\frac{d\eta}{d\eta} \Big) & \scriptstyle{\text{; multivariable chain rule.}}\\
&= -\beta \frac{\partial J(\tau', \theta', \bar{\eta})}{\partial \theta'} \Big( \color{red}{\big(\mathbf{I} + \frac{\partial f(\tau, \theta, \eta)}{\partial\theta}\big)}\frac{d\theta}{d\eta} + \frac{\partial f(\tau, \theta, \eta)}{\partial\eta}\Big) & \scriptstyle{\text{; secondary gradient term in red.}}
\end{aligned} $$
위 식에서 \(\beta\)는 \(\eta\)에 대한 learning rate를 나타낸다.
Meta-gradient RL 알고리즘은 위 식에 빨간색으로 나와있는, \(\mathbf{I} + \frac{\partial f(\tau, \theta, \eta)}{\partial\theta}\)를 0으로 가정해서 연산을 간단하게 만들었는데, 이렇게 하면, parameter \(\theta\)에 대해서 meta-parameter \(\eta\)의 즉각적인 영향을 볼수 있게 된다. 결과적으로 이렇게 하면,
$$ \Delta \eta = -\beta \frac{\partial J(\tau', \theta', \bar{\eta})}{\partial \theta'} \frac{\partial f(\tau, \theta, \eta)}{\partial\eta} $$
논문상의 실험은 meta-objective function을 \(\text{TD}(\lambda)\)와 동일하게 적용시켰는데, 여기서 근사화된 value function \(v_\theta(s)\)와 \(\lambda\)-returnr간의 오차를 줄이게 했다.
$$ \begin{aligned}
J(\tau, \theta, \eta) &= (G^\lambda_\eta(\tau) - v_\theta(s))^2 \\
J(\tau', \theta', \bar{\eta}) &= (G^\lambda_{\bar{\eta}}(\tau') - v_{\theta'}(s'))^2
\end{aligned} $$
Meta-learning the Loss Function
Policy Gradient algorithm에서, expected total reward는 estimated gradient의 방향 내에 포함되어 있는 policy parameter \(\theta\)를 update함으로써 최대화할 수 있다. (Schulman et al, 2016)
$$ g = \mathbb{E}[\sum_{t=0}^\infty \Psi_t \nabla_\theta \log \pi_\theta (a_t \mid s_t)] $$
위 식에서 \( \Psi_t \)는 trajectory return인 \(G_t\)가 될 수도 있고, Q value인 \(Q(s_t, a_t)\), 혹은 advantage value인 \(A(s_t, a_t)\)가 될수도 있다. Policy Gradient를 구하기 위한 surrogate loss function은 다음과 같이 역연산을 해볼 수 있다.
$$ L_\text{pg} = \mathbb{E}[\sum_{t=0}^\infty \Psi_t \log \pi_\theta (a_t \mid s_t)] $$
이 loss function은 과거의 trajectory들에 대한 기록들 ( \(s_0, a_0, r_0, \dots, s_t, a_t, r_t, \dots \))를 대상으로 계산된 것이다. Evolved Policy Gradient (EPG, Houthooft et al, 2018)는 agent가 가지고 있는 과거의 experience \(L_{\phi}\)에 대해서 policy gradient loss function을 (보통 1-D convolution이라고 알고 있는) temporal convolution으로 정의하여 이전의 논문을 조금더 개선했다. 여기서 loss function network의 parameter \(\phi\)는 agent가 더 좋은 return을 얻을 수 있는 방법으로 진화한다.
수많은 meta-learning algorithm과 유사하게, EPG도 두가지의 optimization loop를 가지고 있다.
- Internal loop에서 agent는 가지고 있는 policy \(\pi_{\theta}\)를 개선시키는 방향으로 학습한다.
- Outer loop에서 model은 loss function \(L_{\phi}\)의 parameter \(\phi\)를 update한다. Return과 Loss에 대한 미분함수를 표기할 수 있는 명확한 방법이 없기 때문에, EPG는 Evolutionary Strategies (ES)로 바꿔서 진행한다.
논문의 주요 아이디어는 N개의 agent를 학습시키는 것인데, 각 agent는 \(\phi\)와 \( \epsilon_i \sim \mathcal{N}(0, \mathbf{I}) \) 라는 Gaussian noise를 표준편차 \(\sigma\)를 취한 것으로 결정되는 loss function \( L_{\phi + \sigma \epsilon_i} \) 으로 학습시킨다. Inner loop 학습동안, EPG는 experience에 대한 기록을 계속 가지고 있다가, 각 agent 별로 loss function \( L_{\phi + \sigma \epsilon_i} \)에 따라 policy parameter를 update한다.
$$ \theta_i \leftarrow \theta - \alpha_\text{in} \nabla_\theta L_{\phi + \sigma \epsilon_i} (\pi_\theta, \tau_{t-M, \dots, t}) $$
여기서 \(\alpha_{\text{in}}\)는 inner loop의 learning rate이고, \(\tau_{t-M,\dots,t}\)는 현재의 timestep \(t\)부터 M개의 transition에 대한 기록된 값을 말한다.
이렇게 inner loop에서 학습되는 policy가 충분히 수렴하면, policy는 여러개의 랜덤하게 샘플링한 trajectory들에 대한 평균 return \( \bar{G}_{\phi+\sigma\epsilon_i} \)로 검증을 할 수 있다. 결과적으로 Neural Evolution Strategy (NES)를 활용해서 수치적으로 \(\phi\)에 대한 gradient를 추정할 수 있게 되는 것이다. (Salimans et al, 2017) 이런 과정이 지속되는 동안, policy parameter \(\theta\)와 loss function의 weight \(\phi\)는 더 좋은 return을 얻기 위해서 지속적으로 update된다.
$$ \phi \leftarrow \phi + \alpha_\text{out} \frac{1}{\sigma N} \sum_{i=1}^N \epsilon_i G_{\phi+\sigma\epsilon_i} $$
위의 식에서 \(\alpha_{\text{out}}\)은 outer loop의 learning rate이다.
실제로 loss \(L_{\phi}\)는 (REINFORCE나 PPO같은) 일반적인 policy gradient의 surrogate loss \(L_{\text{pg}}\)와 함께 bootstrapping되어, 다음과 같은 total loss를 구할 수 있게 된다.
$$ \hat{L}_{\phi} = (1-\alpha) L_{\phi} + \alpha L_{text{pg}} $$
여기서 \(\alpha\)는 training동안 1에서 0으로 점차적으로 줄어든다. Test 시점에서는 loss function parameter \(\phi\)는 고정되고, loss value는 policy parameter \(\theta\)를 update하기 위해서 experience에 대한 기록들을 가지고 계산한다.
Meta-learning the Exploration Strategies
Exploitation vs exploration 딜레마는 강화학습에서 아주 중요한 문제이다. Exploration을 하기 위한 일반적인 방법으로는 \(\epsilon\)-greedy나 action에 random noise를 더하는 것, 혹은 action space상에 randomness를 가미한 stochastic policy 등이 있다.
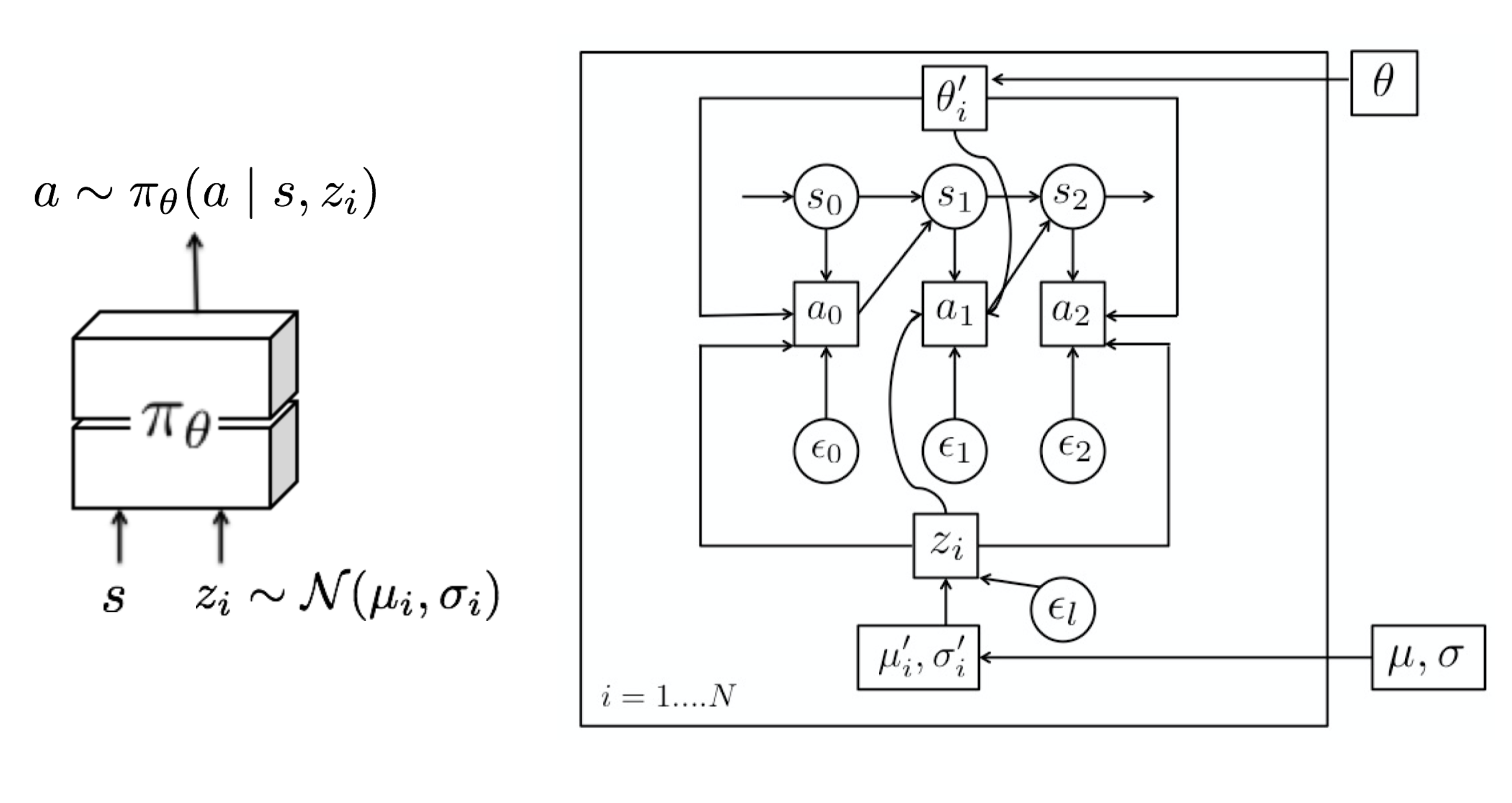
Model Agnostic Exploration with Structured Noise (MAESN) (Gupta et al, 2018) 은 이전에 쌓았던 experience 바탕으로 더 좋고 효율적인 exploration을 위해서 structured action noise를 학습하는 알고리즘이다. 간단하게 random noise를 action에다가 넣는것만으로는 task-dependent하거나 time-correlated한 exploration 방법을 구할 수 없다. MAESN에서는 \(i\)번째 task \(M_i\)마다 task에 따른 random variable \(z_i \sim \mathcal{N}(\mu_i, \sigma_i)\)를 갖는 policy로 변경하여, 이에 따라 변화된 policy \( a \sim \pi_{\theta}(a | s, z_i)\)를 얻어낸다. 여기에 latent variable(내장변수)인 \(z_i\)는 한번 샘플링되고, 샘플링된 시점에서의 에피소드에서는 쭉 고정된다. 직관적으로 놓고 봤을때, 이 latent variable는 에피소드가 진행되는 시점에 더 탐색이 이뤄져야 하고, agent가 이에 따라 action을 결정하는 일종의 behavior(or skill)을 결정하게 된다. 이를 통해서 policy parameter와 내장된 space 모두 total task reward가 커지는 방향으로 최적화된다. 반면, policy는 탐색을 위한 latent variable을 사용하는 방법을 학습하게 된다.
여기에 추가로 loss function은 학습된 latent variable과 unit Gaussian prior간의 KL divergence를 계산하는 값도 포함되어 있다. (\(D_{KL}(\mathcal{N}(\mu_i, \sigma_i) || \mathcal{N}(0, \mathbf{I}))\)) 이 값은 학습된 latent space가 common prior에서 너무 멀리 떨어지지 않게끔 제한을 설정해준다. 또다른 측면에서는 KL Divergence 값은 reward function에 대한 variational Evidence Lower BOund (ELBO) 를 만들어준다. 흥미롭게도 논문에서는 각 task에 대한 (\(\mu_i, \sigma_i\))가 거의 common prior에 가깝게 수렴한다는 것을 보여줬다.
Episodic Control
RL에서 주로 비판의 요소로 잡히는 것이 sample inefficiency이다. Generalization을 최대화하고, 빠른 시점에 학습된 내용에 대해서 까먹는 현상을 막기 위해서 RL의 parameter를 지속적으로 수정하기 위해서는 많은 숫자의 sample과 작은 learning step이 필요하다. (Botvinick et al, 2019)
Episodic control (Lengyel & Dayan, 2008) 논문에서는 빠른 training 내에서 배운 내용에 대해서 까먹는 현상을 막고, generalization을 향상시키는 방법을 제안했다. 부분적으로는 instance 기반의 해마(hippocampal)를 통한 학습에서 발생하는 인지 과정으로부터 아이디어를 가져왔다.
Episodic memory는 과거 시점에 발생한 event들에 대한 기록을 유지하고 있다가, (마치 metric-based meta-learning처럼) 새로운 행동을 해야 하는 시점에서 참고할 수 있는 데이터를 그 기록들을 활용한다. MFEC (Model-Free Episodic Control: Blundell et al, 2016)에서는, memory가 state-action pair \((s, a)\)를 key로 저장하고 이에 해당 Q-value인 \(Q_{EC}(s, a)\)가 value로 저장되는 하나의 큰 table로 설계된다. 만약 새로운 state \(s\)를 받게 된다면, Q-value는 \(k\)개의 가장 유사한 sample들의 Q-value에 대한 평균으로 추정된다.
$$ \hat{Q}_\text{EC}(s, a) =
\begin{cases}
Q_\text{EC}(s, a) & \text{if } (s,a) \in Q_\text{EC}, \\
\frac{1}{k} \sum_{i=1}^k Q(s^{(i)}, a) & \text{otherwise}
\end{cases} $$
여기서 \( s^{(i)}, i=1, \dots, k\)는 \(k\)개의 state \(s\)간의 거리가 짧은 state를 뽑은 것이다. 이후에 이에 대한 action은 가장 높게 추정된 Q-value가 선택한 action을 따르게 된다. 그러면 memory table은 \(s_t\)에 밭았던 return에 따라서 update되게 된다.
$$ Q_\text{EC}(s, a) \leftarrow
\begin{cases}
\max\{Q_\text{EC}(s_t, a_t), G_t\} & \text{if } (s,a) \in Q_\text{EC}, \\
G_t & \text{otherwise}
\end{cases} $$
Tabular RL의 특성상, MEFC는 memory consumption이 많이 발생하게 되고, 유사한 state들끼리간의 generalization을 할 수 있는 방법이 부족했다. 이를 해결할 수 있는 방법이 LRU(Least Recently Use) Cache를 사용하는 것이었다. Matching Network (Vinyals et al, 2016)에 소개된, Metric-based meta-learning에서 아이디어를 얻어서, Generalization 문제는 NEC(Neural Episodic Control, Pritzel et al, 2016)를 통해서 개선시킬 수 있었다.
NEC에 내장된 episodic memory는 Differentiable Neural Dictionary (DND)(참고) 라는 것인데, 여기서 key는 input image pixel에 대한 convolutional embedding vector이고, value는 추정된 Q-value가 들어있다. 주어진 key를 이용해서, 가장 유사한 key들의 값에 대한 weighted sum이 output으로 나오게 되는데, 이 때 weight는 query key와 dictionary내에서 선택된 key간의 kernel measure를 normalize한 것이다. 이런 동작 방식이 일종의 hard attention machanism과 유사하다.

여기서 좀더 나아가, Episodic LSTM (Ritter et al, 2018)은 기본적인 LSTM 구조에 DND episodic memory를 추가한 것인데, 여기서 memory내에는 task context embedding을 key로 저장하고, 이에 따른 LSTM cell의 state를 value로 저장된다. 저장된 hidden state는 기존 LSTM에서 발생하는 gating mechanism과 동일한 과정을 거쳐서 다시 되돌아가 현재의 cell state에 직접적으로 대입된다.
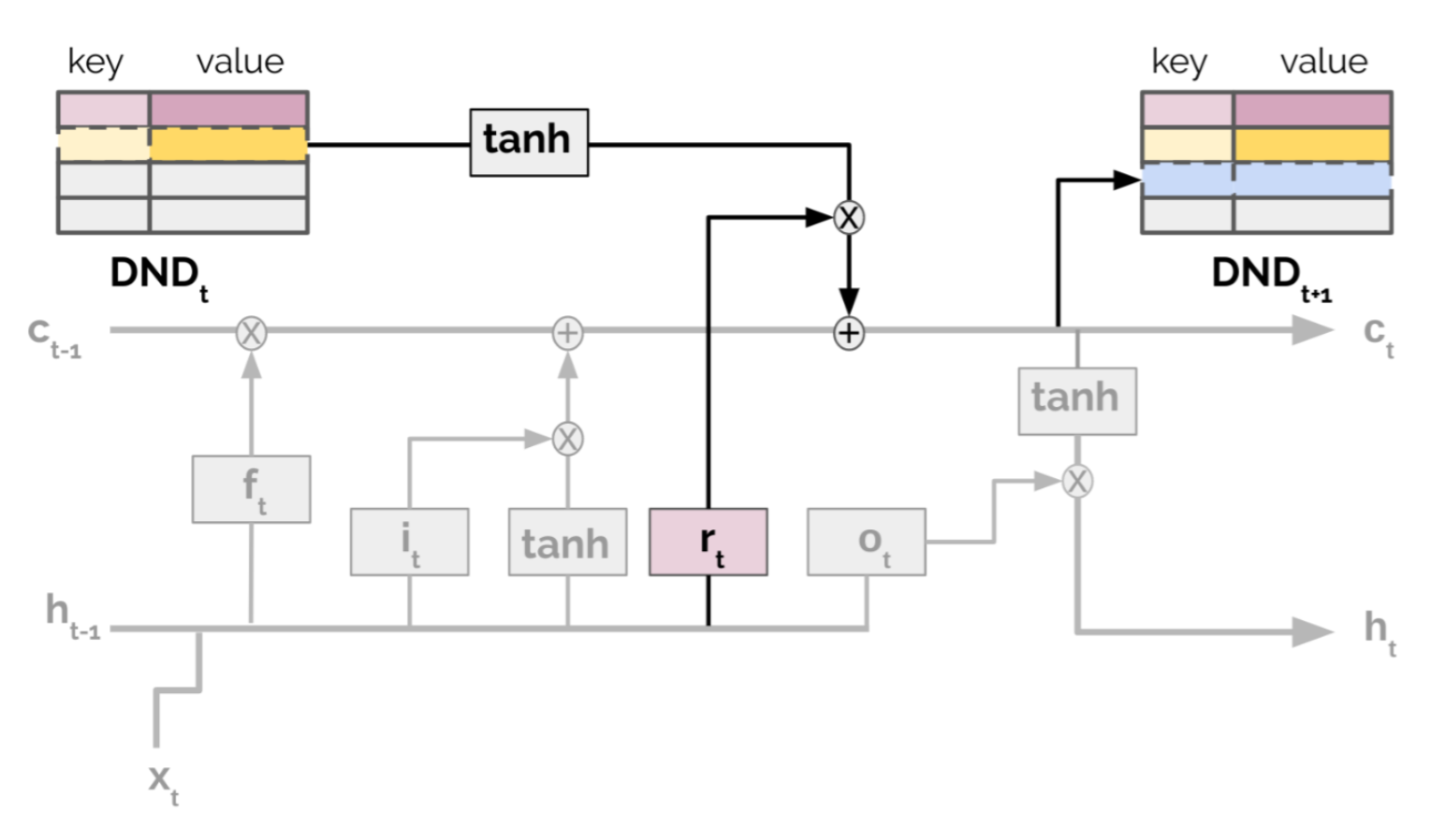
$$ \begin{aligned}
\mathbf{c}_t &= \mathbf{i}_t \circ \mathbf{c}_\text{in} + \mathbf{f}_t \circ \mathbf{c}_{t-1} + \color{green}{\mathbf{r}_t \circ \mathbf{c}_\text{ep}} &\\
\mathbf{i}_t &= \sigma(\mathbf{W}_{i} \cdot [\mathbf{h}_{t-1}, \mathbf{x}_t] + \mathbf{b}_i) & \scriptstyle{\text{; input gate}} \\
\mathbf{f}_t &= \sigma(\mathbf{W}_{f} \cdot [\mathbf{h}_{t-1}, \mathbf{x}_t] + \mathbf{b}_f) & \scriptstyle{\text{; forget gate}} \\
\color{green}{\mathbf{r}_t} & \color{green}{=} \color{green}{\sigma(\mathbf{W}_{r} \cdot [\mathbf{h}_{t-1}, \mathbf{x}_t] + \mathbf{b}_r)} & \scriptstyle{\text{; reinstatement gate}}
\end{aligned} $$
위 식에서 \(\mathbf{c}_t\)와 \(\mathbf{h}_t\)는 time \(t\)에서의 cell state와 hidden state를 의미하고, \(\mathbf{i}_t, \mathbf{f}_t, \mathbf{r}_t\)은 각각 input gate, forget gate, reinstatement gate를 나타낸다. 또한 \(\mathbf{c}_{ep}\)는 episodic memory로부터 뽑아낸 cell state를 의미한다. 새롭게 추가된 episodic memory 요소는 위 식에서 초록색으로 표기되었다.
위의 구조는 context 기반의 다시 받은 정보를 통해서 이전 experience의 요약된 내용을 알려준다. 반면, 외부 메모리에 저장된 task-dependent한 experience는 기존 데이터가 잊혀지는 현상을 막는다. 논문 내에서, 모든 실험은 일일이 만든 context vector를 가지고 이뤄졌다. 더 자유로운 형태의 task들에 대해서 task context embedding를 얼마나 효과적이고 효율적으로 만드는 방법도 하나의 흥미있는 주제가 될거 같다.
전체적으로 episodic control의 성능은 environment의 complexity에 따라 제한된다. agent 입장에서는 real-world task상에서 같은 state에 반복적으로 정확히 방문하는 것은 매우 드물기 때문에, state를 적절하게 encoding하는 것이 중요하다. 이렇게 학습된 embedding space는 observation data를 낮은 차원의 space로 압축시키는 한편, 해당 space에 들어 있는 유사한 state들은 유사한 strategy를 따르게끔 되어있다.
Training Task Acquisition
위에서 언급한 3가지 핵심 요소 중에서, task의 분포를 어떻게 적절하게 설계하느냐는 아직 많이 연구되지 않은 부분이기도 하고, 어쩌면 meta-RL 자체에 가장 부합하는 요소일거라 생각하낟. 위에서 전제를 둔 것처럼, 각 task는 MDP로 구성되어 있다.(\(M_i = \langle \mathcal{S}, \mathcal{A}, P_i, R_i \rangle \in \mathcal{M}\)) 이런 task들의 MDP에 대한 분포를 아래와 같이 수정함으로썬 만들어볼 수 있다.
- Reward Configuration : 서로 다른 task들간에, 같은 action도 \(R_i\)에 따라서 다르게 reward가 다르게 주어질 수 있다.
- Environment : transition function \(P_i\)도 state간에 shift를 다르게 한 environment를 초기화함으로써 형태를 바꿀 수 있다.
Task Generation by Domain Randomization
Simulator내의 parameter를 랜덤화시키는 것은 수정된 transition function을 가진 task를 구할 수 있는 쉬운 방법이다. 이 부분에 대해서 더 확인해보고 싶다면 domain randomization에 관한 포스트(번역)를 확인해보면 좋다.
Evolutionary Algorithm on Environment Generation
Evolutionary algorithm은 natural selection에서 영감을 얻은, gradient 없이 heuristic하게 구하는 최적화 방법이다. Solution을 구하는 과정은 평가(Evaluation), 선택(Selection), 재생성(Reproduction), 그리고 변이(mutation)의 과정을 거친다. 결과적으로 좋은 solution만 남고, 해당 solution이 선택된다.
POET (Wang et al, 2019) 은 evolutionary algorithm 기반의 framework로써, 문제들이 스스로 풀리는 동안 관련 task를 계속 생성해낸다. POET은 특별히 설계된 2D 환경의 bipedal walker에서만 구현되어 있지만, 좋은 방향을 제시하고 있다. 주목할만한 부분은 evolutionary algorithm이 앞에서 소개한 EPG나 PBT (Population-Based Training, Jaderberg et al, 2017)와 같이 Deep learning과 접목되어 좋은 결과를 보여주는 것들이 있다는 것이다.

2D bipedal walking environment는 진화되는 형태로 되어 있다. 그래서 단순히 평평한 표면부터 임의의 gap, stump, terrain의 거친 정도와 같이 어려운 경로로 구성되어있다. POET에서는 환경 측면에서 극복해야할 문제와 해당 환경에서 agent가 최적화된 내용을 쌍으로 묶어서 (a) 현재의 극복해야할 문제를 해결할 수 있게끔 agent를 선택하고, (b) 해당 환경을 해결할 수 있게끔 진화시켜준다. Algorithm에서는 environment-agent pair를 가지고 있으면서, 다음 과정을 반복하게 된다:
- Mutation : 현재 활성화되어 있는 환경으로부터 새로운 환경을 만들어낸다. 유념할 부분은 mutation operation의 종류를 생성하는 것은 bipedal walker를 위해서만 발생하는 것이고, 새롭게 생성된 환경은 새로운 설정값을 가질 것이다.
- Optimization : 선택된 환경 내에서 쌍으로 묶여있는 agent를 학습시킨다.
- Selection : 주기적으로 현재 학습된 agent의 환경을 다른 환경으로 한번 옮겨본다. 각 환경에서 가장 좋은 성능을 보인 agent를 복사하고, update시킨다. 여기서 확인하고자 하는 부분은 한 환경에서 학습된 skill같은 것은 다른 환경에서도 도움이 될 것이라는 가정이다.
위에서 소개한 과정은 PBT와 매우 유사하지만, PBT에서는 hyperparameter를 변이시키고, 진화시킨다. 부연 설명을 하자면, POET은 domain randomization을 수행하는 것이고, 모든 gap, stump, terrain의 거친 정도는 특정 randomization probability parameter에 의해서 결정된다. Domain Randomization과 다른 부분은, agent가 한번에 완전 랜덤한 어려운 환경에 노출되지 않는다는 것이고, 대신 evolutionary algorithm에 의해서 설정된 계획에 따라서 지속적으로 학습된다는 것이다.
Learning with Random Rewards
reward function \(R\)이 없는 MDP를 보통 Controlled Markov Process (CMP)라고 표현한다. 주어진 CMP \(<S, A, P>\)에서는 효율적인 meta-learning policy를 학습시킬 수 있도록 도와주는 여러 reward function \(R\)들을 생성함으로써 다양한 task들을 얻어낼 수 있다.
Gupta et al, 2018에서는 CMP에서 task distribution을 확장시킬 수 있는 두가지 unsupervised 방식을 제안했다. 만약 모든 task와 연관되어 있는 주어진 latent variable \(z \sim p(z)\)이 있다고 가정했을때, 해당 값을 이용해서 reward function을 조절하거나 정의할 수 있다 (\(r_z(s) = \log D(z|s)\)), 여기서 \(D(\dot)\)은 "discriminator" 함수인데, state로부터 latent variable을 뽑는데 사용한다. 논문에서는 discriminator function을 만드는 방법으로 두가지를 소개했다.
- Discriminator function에 대한 random weight \(\phi_{rand}\)를 샘플링한다: \(D_{\phi_{rand}}(z|s)\)
- 다양성 위주의 exploration을 하기 위한 discriminator function을 학습한다. 이 방법은 또다른 논문인 "DIAYN" (Eysenbach et al, 2018)에서 자세하게 소개되어 있다.
"Diversity Is All You Need"의 줄임말인 DIAYN은 policy가 reward function 없이도 유용한 skill을 학습할 수 있게끔 도와주는 framework이다. 여기서는 latent variable \(z\)를 skill embedding으로 모델링하고, policy를 \(z\)에 state \(s\)를 붙인 형태로 만들어준다.( \(\pi_{\theta}(a|s, z)\)) (이 부분은 앞에서 소개한 MAESN의 과정과 동일하다.) DIAYN의 구조는 몇가지 추론으로부터 나왔다.
- Skill은 반드시 다양해야 하며, 이로 인해서 서로 다른 state들을 방문할 수 있어야 한다. 이를 통해 state와 skill간의 잠재적인 정보 (\(I(S;Z)\)) 를 최대화할 수 있다.
- Skill은 action이 아닌 state에 의해서 구분이 가능해야 한다. 이를 통해서 state에 의해서 제한되는 환경상에서 action과 skill간의 잠재적인 정보 (\(I(A;Z | S)\))를 줄일수 있다.
최대화시켜야 할 Objective function은 다음과 같이 정의되는데, diversity를 더 넓히기 위해서 policy entropy항이 더 추가된다.
$$ \begin{aligned}
\mathcal{F}(\theta)
&= I(S; Z) + H[A \mid S] - I(A; Z \mid S) & \\
&= (H(Z) - H(Z \mid S)) + H[A \mid S] - (H[A\mid S] - H[A\mid S, Z]) & \\
&= H[A\mid S, Z] \color{green}{- H(Z \mid S) + H(Z)} & \\
&= H[A\mid S, Z] + \mathbb{E}_{z\sim p(z), s\sim\rho(s)}[\log p(z \mid s)] - \mathbb{E}_{z\sim p(z)}[\log p(z)] & \scriptstyle{\text{; can infer skills from states & p(z) is diverse.}} \\
&\ge H[A\mid S, Z] + \mathbb{E}_{z\sim p(z), s\sim\rho(s)}[\color{red}{\log D_\phi(z \mid s) - \log p(z)}] & \scriptstyle{\text{; according to Jensen's inequality; "pseudo-reward" in red.}}
\end{aligned} $$
위 식에서 \(I(\dot)\)은 잠재 정보를 말하고 \(H[\dot]\)은 entropy measure를 말한다. 여기서 \(p(z|s)\)를 계산하기 위해서 모든 state를 모을 수 없기 때문에 이 값을 앞에서 소개한 diversity-driven discriminator function 인 \(D_{\phi}(z|s)\)로 근사시킨다.

한번 discriminator function이 학습되면, training을 위한 새로운 MDP를 sampling하는 것은 매우 직관적이 된다. 우선 latent variable \(z \sim p(z)\)를 샘플링하고 이를 이용해서 reward function \(r_z(s) = \log (D(z|s))\)를 만들어낸다. 이 reward function을 앞에서 가정한 CMP와 쌍으로 묶으면 이게 새로운 MDP가 된다.
해당 포스트 글을 논문에 인용하려면 다음 bibtex를 참고하고, 포스트와 관련해서 오류나 문제가 발생하면 댓글이나 원저자 (lilian dot wengweng at gmail dot com), 혹은 역자(kcsgoodboy at gmail dot dom) 에게 문의해주시면 감사하겠습니다.
@article{weng2019metaRL,
title = "Meta Reinforcement Learning",
author = "Weng, Lilian",
journal = "lilianweng.github.io/lil-log",
year = "2019",
url = "http://lilianweng.github.io/lil-log/2019/06/23/meta-reinforcement-learning.html"
}
'Study > AI' 카테고리의 다른 글
| [TIP] Jupyter에서 서버상의 데이터를 읽어오기 (0) | 2020.01.15 |
|---|---|
| [DL] Types of Computer Vision Models (0) | 2020.01.08 |
| [DL] Pre-Trained Model in OpenVINO (0) | 2020.01.07 |
| [RL] Linear TD (0) | 2019.11.12 |
| [RL] The Objective of TD (0) | 2019.11.12 |
| [RL] The Objective for On-policy Prediction (0) | 2019.11.11 |
| [RL] Estimating value function with supervised learning (0) | 2019.11.06 |
- Total
- Today
- Yesterday
- Kinect
- Variance
- bias
- 인공지능
- 강화학습
- Windows Phone 7
- DepthStream
- 딥러닝
- reward
- arduino
- Pipeline
- windows 8
- TensorFlow Lite
- Policy Gradient
- Gan
- Off-policy
- ColorStream
- SketchFlow
- RL
- Kinect SDK
- processing
- End-To-End
- Offline RL
- 파이썬
- PowerPoint
- Distribution
- Expression Blend 4
- dynamic programming
- 한빛미디어
- Kinect for windows
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
