티스토리 뷰
(해당 포스트는 Coursera의 Prediction and Control with Function Approximation의 강의 요약본입니다)
이전 포스트까지 다룬 알고리즘들은 기본적으로 state/action에 따른 value가 table 형식으로 정의된 tabular value function을 사용했다. 이런 케이스 value function을 정의하기는 쉽지만, 일반화(generalization)을 하기가 어렵다. 예를 들어서 action이나 state가 table처럼 구분할 수 있는 discrete한 값이 아니라 continuous한 값을 가진 경우라면, 위와 같은 tabular value function을 사용하기 어렵다. 또한 state space나 action space의 scale이 매우 작아서 table 자체가 엄청 커지게 되면, 이 table을 저장할 만한 저장공간도 고려해야 한다.
결국 이를 해결하는 방법이 table 자체를 일종의 수식으로 근사(approximation)하자는 것이다. 그러면 굳이 table을 위한 저장 공간을 확보하지 않더라도, 우리가 기존에 활용했던 것처럼 state/action을 넣어주면 이에 맞는 value를 return해주면 어느정도 value function으로써 활용하기 좋을 것이다.(물론 근사가 된 이상, 정확하지는 않을 것이다.)
$$ \hat{v}(s, \mathbf{w}) \approx v_{\pi}(s) $$
대신 우리가 처음부터 이 value function을 아는 것은 아니니까, 이 value function을 보정해주기 위한 weight \( w\)이 하나의 인자로 들어가게 된다. 이를 통해서 \(w\)에 의해서 value function이 결정되는 일종의 parameterized value function을 만든 것이다. 이런 Linear function을 만들어가는 과정 자체를 Linear Value Function Approximation이라고 표현한다. 수식적으로는 아래와 같이 표현된다.
$$ \begin{align} \hat{v}(s, \mathbf{w}) & \doteq \sum{ w_i x_i(s) }\\
&= < \mathbf{w}, \mathbf{x}(s) > \end{align} $$
참고로 \( x_i(s) \)는 해당 state \(s\)에서의 feature들을 말하는 것이고, 행렬의 inner product로 보여주기 위해서 \(\mathbf{x}(s) \)꼴로 표현하기도 한다. 이러면 \(\mathbf{x}(s) \) 는 말그래도 feature vector가 되는 것이다. 물론 이렇게 Linear function으로 정의할 수 없는 경우에는 위와 같은 Linear Value Function Approximation도 할 수 없다. 이런 경우는 보통 주어진 feature로는 value function을 정의할 수 없다고 표현하고, 새로운 feature를 찾아야 한다. 아니면 위와 같은 Linear function으로 근사하는 방식이 아닌, Non-linear function으로 근사하는 방법이 있을텐데, 이 때 Neural Network를 활용하게 된다. 그러면 이에 대한 도식은 아래와 같이 된다.
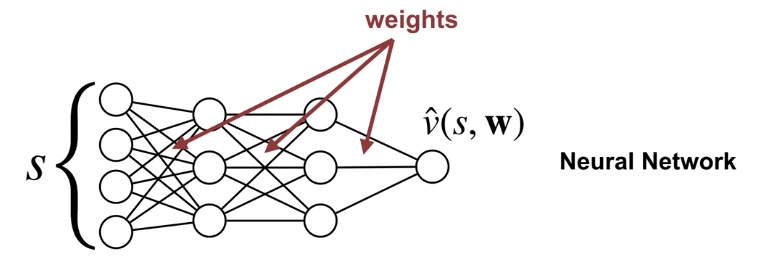
그래서 많이 알려져 있는 Deep Q Network (DQN) 같은 알고리즘은 Function Approximator를 Neural Network로 구현한 것이고, 이런식으로 Value Function을 근사하는데 Neural Network를 사용한 알고리즘들을 모두 Deep Reinforcement Learning이라고 표현한다. (물론 Q-learning에서 Neural Network을 사용한 계열이고, Policy Gradient method에서 Nerual Network을 사용한 케이스도 Deep Reinforcement Learning의 범주에 있다.)
그러면 어떻게 Value Function을 Approximation해야 잘되었다고 표현할까? 큰 관점에서는 앞에서 잠깐 언급한 Generalization과 Discrimination 측면으로 나눠 볼 수 있다. Generalization은 말그대로 사람이 목표와 유사한 Task를 학습하는 경우와 같이 value function이 모든 state에 대해서 일반화가 되었냐를 표현하는 것이다. 예를 들어서 사람이 차를 운전하는 것을 학습하는 경우도 꼭 모든 종류의 차에서 운전할 필요없이 하나의 차종에서 학습하면, 나머지 차종에 대해서도 일반화가 되어 잘 운전할 수 있는 것이다. 이뿐만 아니라 모든 장소에 대해서 운전을 학습할 필요없이, 도로의 유형에 대해서만 학습이 되면 어느정도 운전이 가능한 것도 마찬가지 경우이다. 좀 다르게 표현하자면 어떤 value function이 정의되었을때, 특정 state의 value가 update되었을 경우 이런 경향이 다른 state의 value에도 영향을 끼치는 것이다. 만약 generalization이 잘 된 value function이라면 그만큼 기존 정보만 활용해서도 실제와 유사한 value function에 근사가 될 것이므로 학습이 조금더 빨라질 것이다.
반면 Discrimination은 단어뜻 그대로 차별성을 나타낸다. 그래서 state가 여러개 있을 때, 이 state들에 대한 value들간에 얼마나 차이가 있는지를 표현하는 것이다. 상식적으로 state가 다른 이상, 이에 대한 value들도 달라야 하며, 만약 discrimination이 잘된 value function으로 학습된 agent라면 주어진 state에 대해서 각각 취할 수 있는 policy의 범주가 넓어질 것이다. 즉, 이 또한 학습이 잘되게 하는 하나의 요소가 될 수 있는 것이다.
당연히 좋은 Function Approximation을 이루기 위해서는 Generalization도 잘 되어야 하고, Discrimination도 잘 되어야 한다. 그런데 위의 설명을 보면 알겠지만, 두개 요소에 대한 trade-off가 존재한다. Discrimination이 잘 이뤄지려면, 가능한한 state도 세분화해야 될텐데, 이렇게 되면 당연히 Generalization 성능은 떨어질 것이다. 반면 Generalization을 잘 하기 위해서 그냥 모든 state에 대해서 평균을 취한다던지 하나로 뭉뚱그려서(aggregate) 이에 대한 value를 따지게 된다면, 정확한 state에 대한 value를 얻기는 힘든만큼 Discrimination 성능은 떨어질 것이다. 그래서 되도록이면 이런 특성을 고려하면서 high generalization, high discrimination을 이루는 Function Approximation을 구현해야 한다. 가령 어느정도 유사한 state에 대해서는 묶어서 표현하고, 그래도 구분이 되는 state끼리는 분리한다던지 말이다.
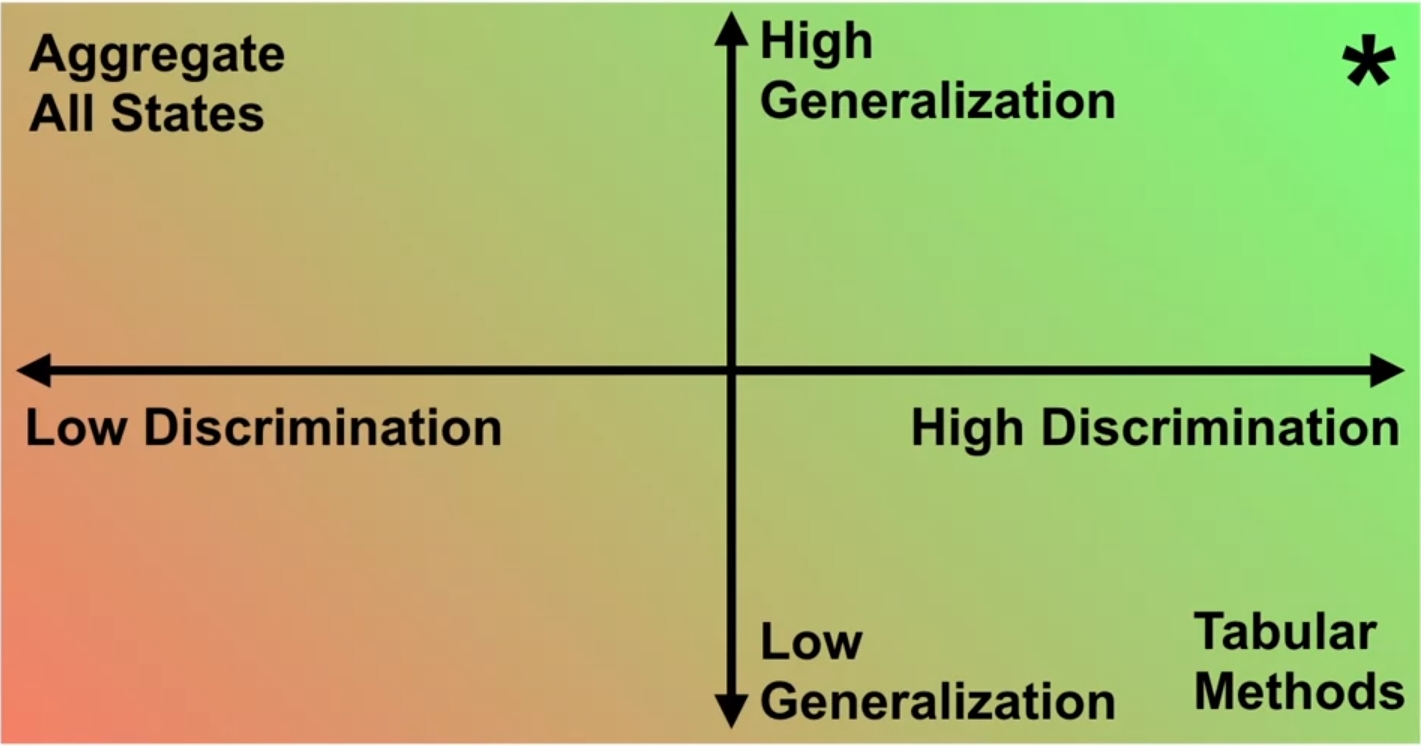
일단 위의 방식들이 제시한 Value function approximation이 쉽지는 않겠지만, 이 문제를 일종의 Supervised Learning의 하나라고 바라보면 Value function을 근사하는 것도 어느정도 가능해진다. 아마 머신러닝이나 딥러닝 공부를 하면 제일 먼저 다루는 예제가 Boston House Price 일텐데, 이 문제도 주어진 dataset을 사용해서 linear regression을 통해 집값을 예측하는 일종의 함수를 만들어낸다. 이처럼 뭔가 state value에 대한 관계를 확인할 수 있는 dataset이 있으면 value function을 근사할 수 있을 것이다.
사실 이전에 다뤘던 Monte Carlo method나 TD Learning 같은 경우도 같은 접근 방식을 취할 수 있다. Monte Carlo method를 취하게 되면, 주어진 policy \(\pi\)에 대한 value function을 추정하는 Policy Evaluation이라는 과정이 있었다. 이때 state에 대한 return을 샘플링해서 value function을 구할텐데, 앞에서 언급한 방법대로라면 이 state에 대한 return을 하나의 dataset으로 보고 value function을 학습시킨다면 어느정도 실제 value function에 근사한 결과가 나올 것이다. 물론 이때 value function의 input은 state가 될 것이고, output은 해당 state에서 termination되었을 때까지 얻은 총 return (\(G\)) 이 되겠다. 이 값이 expected return과 가까워지면 우리가 추구하는 목적을 달성할 수 있게 될 것이다.
TD Learning에서도 마찬가지이다. Monte Carlo Method에선 total return을 썼지만, TD Learning에서는 1-step bootstrapping된 return을 썼기 때문에 total expected return도 \(R + \gamma \hat{v}(S, \mathbf{w})\)의 형태로 나온다. 그렇기 때문에 앞의 형태처럼 input은 state인 상태에서 output만 바뀐 function을 찾는게 목적이 될것이다.

하지만 이렇게 Supervised Learning 방법을 그대로 Function Approximation을 Policy Evaluation에 적용할 수 있는 것은 아니다. 앞에서 다뤘던 boston price prediction의 경우도 집값을 예측하는 모델이 동일한 가정하에서 학습을 진행하는데, 위와 같은 Function Approximation도 학습하는 agent가 동일한 환경내에서 state에 대한 expected return을 얻은 경우에만 적용된다. 물론 Function Approximation시 필요한 dataset도 같은 모델에서 나와야 한다. 보통 이런 설정을 online setting이라고 한다. 반대의 케이스인 offline setting은 dataset이 그냥 특정 주기내로 고정된 형태를 말한다. 간단하게 설명하자면, Function Approximation을 통해서 어떤 linear function을 도출했다고 가정할 때 online setting인 경우는 주어진 dataset을 바탕으로 학습이 되고, 새롭게 들어온 data를 가지고 linear function을 update할 수 있다. 반면 offline setting의 경우는 이미 전체 데이터가 주어진 상태에서 linear function이 approximation될 뿐, 새로운 dataset을 통해서 update될 여지가 없기 때문에 function approximation을 할 이유가 없어진다. 이때문에 Function approximation은 online setting이 된 상태에서만 유의미하다고 보면 좋을거 같다. (참고로 Online setting과 Offline setting의 차이는 여기를 살펴보면 좋을 거 같다.)
TD Learning은 한가지를 조금더 유심히 살펴봐야 한다. 사실 Monte Carlo method의 경우는 total return \(G\)를 이용해서 바로 Function Approximation이 가능하지만, 대신 알다시피 total return을 구하기 위해서 episode가 끝날때까지 기다려야 한다. 이 문제를 해결하기 위해서 TD Learning에서는 (특히 TD(0)에서는) 1-step bootstrapping method를 적용해 total return을 구했지만 문제는 이 total return도 value function을 바탕으로 계산되기 때문에 target이 Function Approximation때 결정되는 weight \( \mathbf{w} \)의 영향을 받게 된다는 것이다.
$$ \begin{align} \text{original TD : } & R + \gamma V(s) \\
\text{TD with Function Approx. : } & R + \gamma \hat{v}(S, \mathbf{w}) \end{align} $$
보통 Supervised Learning은 위와 같이 target이 변하는 경우를 해결하는 방법이 아니기 때문에 이 경우는 다른 방법을 고민해봐야 한다. 책에서는 TD Learning에 Gradient를 접목한 Semi-Gradient TD(0) 같은 방식을 소개하는데, 이 부분도 다음 포스트에서 다룰 예정이다.
'Study > AI' 카테고리의 다른 글
| [RL] Linear TD (0) | 2019.11.12 |
|---|---|
| [RL] The Objective of TD (0) | 2019.11.12 |
| [RL] The Objective for On-policy Prediction (0) | 2019.11.11 |
| [RL] Dealing with inaccurate models (0) | 2019.10.08 |
| [RL] Dyna as a formalism for planning (3) | 2019.09.30 |
| [RL] Model & Planning (0) | 2019.09.25 |
| [RL] Expected SARSA (0) | 2019.09.18 |
- Total
- Today
- Yesterday
- processing
- 강화학습
- Variance
- 딥러닝
- RL
- Kinect
- windows 8
- arduino
- Kinect SDK
- Policy Gradient
- 파이썬
- ColorStream
- 인공지능
- Pipeline
- Kinect for windows
- Windows Phone 7
- SketchFlow
- 한빛미디어
- Distribution
- Offline RL
- reward
- dynamic programming
- PowerPoint
- bias
- DepthStream
- Expression Blend 4
- Off-policy
- End-To-End
- Gan
- TensorFlow Lite
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
