티스토리 뷰
[RL][Review] Offline Reinforcement Learning From Algorithms to Practical Challenges
생각많은 소심남 2022. 4. 27. 13:25(본문의 의도를 가져오되, 개인적인 의견이 담길 수도 있습니다.)
Offline Reinforcement Learning from Algorithms to Practical Challenges - Kumar et al, NeurIPS 2020 Tutorial (사이트, 실습코드)
원래 거진 3시간짜리 tutorial이기 때문에 정리하는데 시간이 걸릴듯 하다. 그래도 전반적인 Offline RL의 문제와 이론에 대해서 잘 설명되어 있어서 차근차근 설명해보고자 한다. 기본적인 RL 내용도 포함되어 있어, Offline RL 부분만 뽑아서 정리한다.
Can we develop data-driven RL methods?
보통 강화학습이라고 하면 다음과 같은 환경을 가정하고 진행한다.
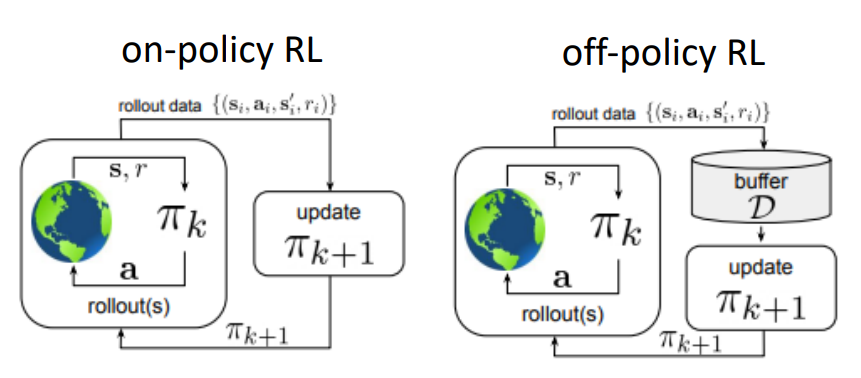
일반적으로는 어떤 환경이 주어져 있고, 그 환경 상에서 학습시키고자 하는 에이전트가 존재할 때 이 에이전트가 직접 환경과 interaction을 수행하면서 얻은 경험을 바탕으로 policy를 형성하는 형태로 되어 있다. 이때 policy를 배울때의 정보의 원천이 환경이냐, 아니면 환경에서 수집한 데이터의 집합이 저장된 replay buffer로부터 학습하냐에 따라서 on-policy / off-policy를 구분할 수 있다. 특히 off-policy에서는 replay buffer에 저장할 정보를 수집할 policy와 이 정보를 가지고 학습시킬 policy를 behavior policy와 target policy로 나눠서 표현을 하곤한다. 두 방식 모두 실제 environment와 interaction이 이뤄져야 하며, interaction을 하면서 새롭게 쌓은 정보를 통해 policy를 개선하는 과정을 포함하고 있다. 그래서 실제 환경과는 계속 연결되어 있어야 하며, 이때문에 이런 부류의 학습을 online reinforcement learning이라고 정의한다.
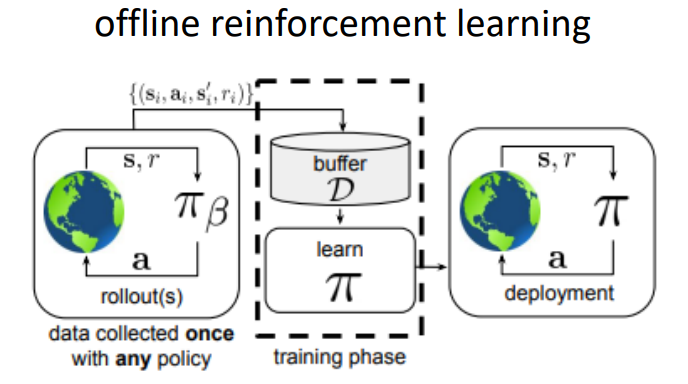
반면 offline reinforcement learning은 기본적으로 환경과의 interaction이 없는 것을 가정한다. 이 말은 즉, policy improvement 과정을 위해 새로운 정보가 저장될 기회가 없다는 것이다. 그러면 상식적으로 생각해도 policy를 학습시킬 데이터가 어마어마해야 하며, 그 데이터에는 적어도 환경의 변화를 묘사할 수 있는 다양성이 존재해야 할 것이다. 그래서 offline RL논문을 보면 많이 나오는 단어가 static, fixed dataset이라는 단어다. 대신 이 데이터의 원천에 대해서는 제한을 두지 않는다. 예를 들어서 agent가 policy를 수행하면서 수집한 데이터가 아니더라도, 사람이 해당 환경에서 action을 취한 결과나 다른 policy가 쌓은 정보라도 모두 fixed dataset의 범주에 포함시킬 수 있다. (그림 상에서는 이를 따로 \(\pi_{\beta}\)로 표현하고 있다. 조금 살펴보면 off-policy에서의 policy는 \(\pi_k\)로 표현되어 있어 이 부분이 다른 것을 확인할 수 있다) 그리고 이렇게 학습된 policy를 이제 실제 환경에 deploy하는 과정이 될텐데, 이 때 쌓은 새로운 데이터를 기존의 fixed dataset에 추가해서 기존의 policy를 개선시키는 방법도 존재할 것이다. 만약 이런 방법론이 유용하다면 당연히 data-driven RL도 구현할 수 있는 셈인데, 사실 개념 자체는 옛날에도 batch RL 이란 이름으로 알려져 왔던 것이다. 그리고 이게 실제로 가능하다면 기존에는 강화학습으로는 불가능하다고 생각했던 영역에 접목시킬 수 있게 될 것이다. 예를 들어서 자율주행이나 의학 분야에서는 exploration에 따른 cost가 매우 큰 편인데, 이와 같이 dataset에서 학습할 수 있다면, 또한 expert data도 학습에만 활용할 수 있다면 좋지 않을까...
What does offline RL mean?
Offline RL problem을 공식화하면 다음과 같다. 우선 dataset \(\mathcal{D} = \{(s_i, a_i, s_i', r_i)\}\) 가 존재하고, 이 dataset은 behavior policy \(\pi_{\beta}\)에 의해서 수집되었다. (참고로 \(\pi_{\beta}\)는 우리가 모르는 policy라는 것을 가정한다) 이때 \(s\)와 \(a\)는 다음과 같은 관계로 표현할 수 있다.
$$ s \sim d^{\pi_{\beta}}(s) \\ a \sim \pi_{\beta}(a \vert s) \\ s' \sim p(s' \vert s, a) \\ r \leftarrow r(s, a)$$
물론 강화학습으로 해결하고자 하는 문제는 명확하다. 당연히 에이전트가 쌓는 expected reward의 총합을 크게 만드는 것이다.
$$ \max_{\pi} \sum^T_{t=0} \mathbb{E}_{s_t \sim d^{\pi}(s), a_t \sim \pi (a \vert s)} [ \gamma^t r(s_t, a_t)] $$
여기서 \(\pi\)는 앞의 \(\pi_{\beta}\)가 아닌, 실제 환경에서 수행할 policy \(\pi\)이다. 그러면 강화학습을 조금 공부해본 사람이라면 이런 질문을 던질 수 있다. 실제 환경에서 수행될 policy와 학습된 policy가 다른데 이게 잘 동작할까.. 하고 말이다. 예를 들면 수능을 보는데 모의고사 볼때는 쉬운문제를 먼저 푸는 전략을 취하는데, 막상 수능에서는 시간이 많이 걸리는 문제가 많이 나와서 전략이 어긋나는 정도?
How is this even possible?
그러면 이런 offline 설정이 잘 동작하게 만드는 요인이 있을까? 간단하게 다음 세가지 요인을 꼽을 수 있다.
- dataset이 무척 크다면 그 안에는 좋은 action과 나쁜 action들이 있을 것이고, 그 dataset내에는 어느 정도 좋은 action에 대한 경향을 찾을 수 있다는 점이다. 이는 당연히 임의로 동작하는 방식보다는 좋은 결과를 보여줄 것이다.
- Generalization: 일반화 관점에서 살펴보면, 일반적으로 어떤 환경에서의 좋은 action은 다른 환경에서도 좋은 action일 가능성이 크다.
- Stitching: Stitching이라는 것은 말 그대로 바느질을 말하는데, 이는 부분적인 action들을 적절히 조합해서 좋은 action을 찾을 수 있다는 것을 표현하는 것이다. 예를 들어서 어떤 환경이 A에서 B를 거쳐 C로 가는 문제를 가지고 있는 상황에서 에이전트가 직접적으로 A에서 C로는 가는 정책을 학습하지 못했더라도,부분적으로 A에서 B로 가는 정책과 B에서 C로 가는 정책을 학습했다면 이를 적절히 조합해서 좋은 정책을 만들어낼 수 있을 것이다.
위의 요소들이 바로 offline 설정에서 찾을 수 있는 속성인 것이다.
Does it work?
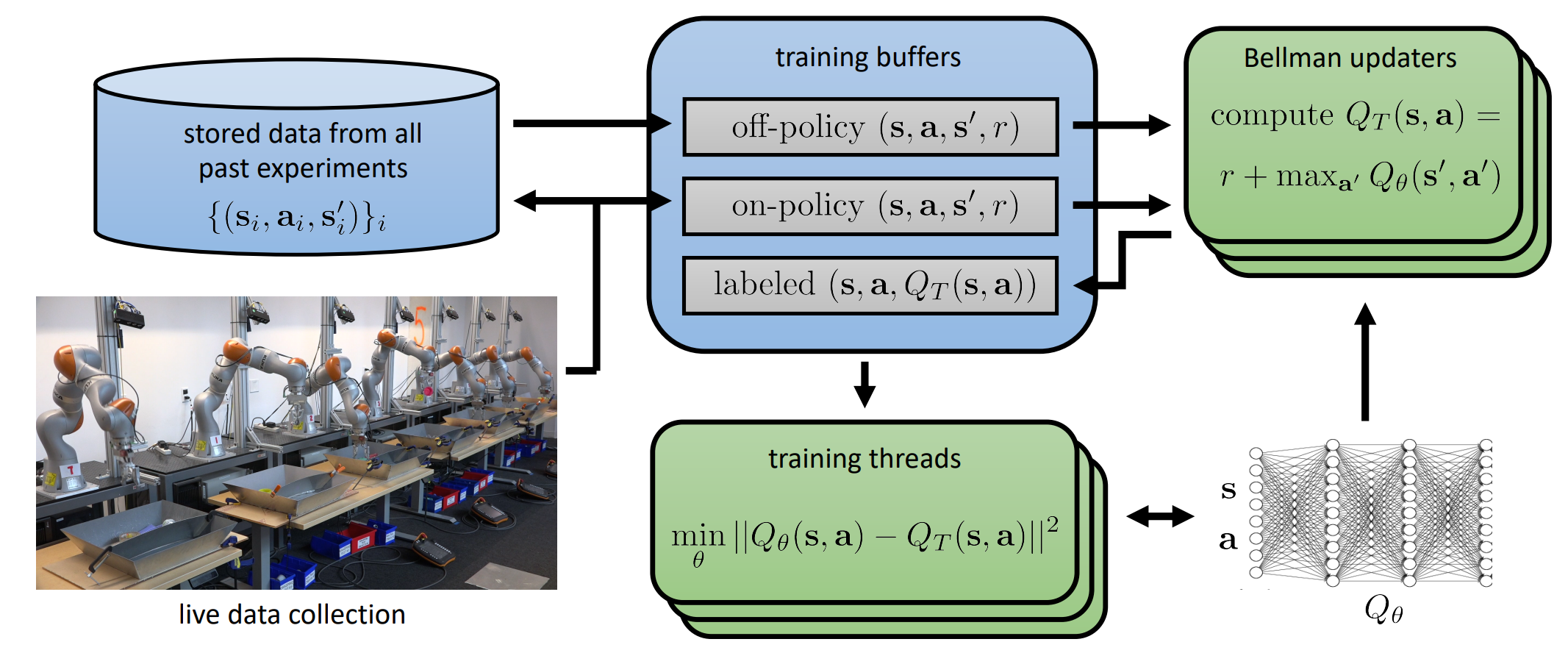
이런 방식은 실제로 적용했을 때도 꽤 잘 동작했다. 위의 그림은 Levine 교수랩에서 발표한 QT-opt 라는 알고리즘인데, 이 알고리즘을 robot grasping 작업 학습시 쓰면서 offline 설정을 적용했다. 그림에서는 stored data from all past experiments 라고 되어 있는 부분이 앞에서 언급한 fixed dataset인 것이다. (물론 학습에는 이 데이터 뿐만 아니라 fine-tuning을 위한 online data도 포함되어 있긴 하다) 논문에서는 어떤 물건을 집는 방법에 대해서 학습시키고, 학습되지 않은 물건을 집으라고 했을때 잘 되는지에 대한 실험을 했었고, 이를 offline dataset만을 썼을 때와 online dataset을 혼합한 결과를 비교했다.

여기서 주목할 부분은 offline dataset에 비해서 작은 규모의 online dataset을 추가했음에도 Failure rate가 offline dataset만 사용한 것에 비해 1/3로 절감되었다는 것이다. 결과적으로 이는 dataset의 크기보다는 다른데 문제가 있다는 것을 알 수 있다. (참고로 offline dataset 자체는 이미 매우 좋은 것이라는 것을 가정해둔다)
Why is offline reinforcement learning hard?
그러면 어떤 부분이 offline rl 의 성능을 저하시키는 것일까? 우선 feedback의 유무를 들 수 있다. 강화학습의 특성상 어떤 model이나 policy를 학습할때는 특정 action을 취했을 때 환경의 변화를 관찰해야 하는데, offline 설정에는 이런 것이 제한적이다.
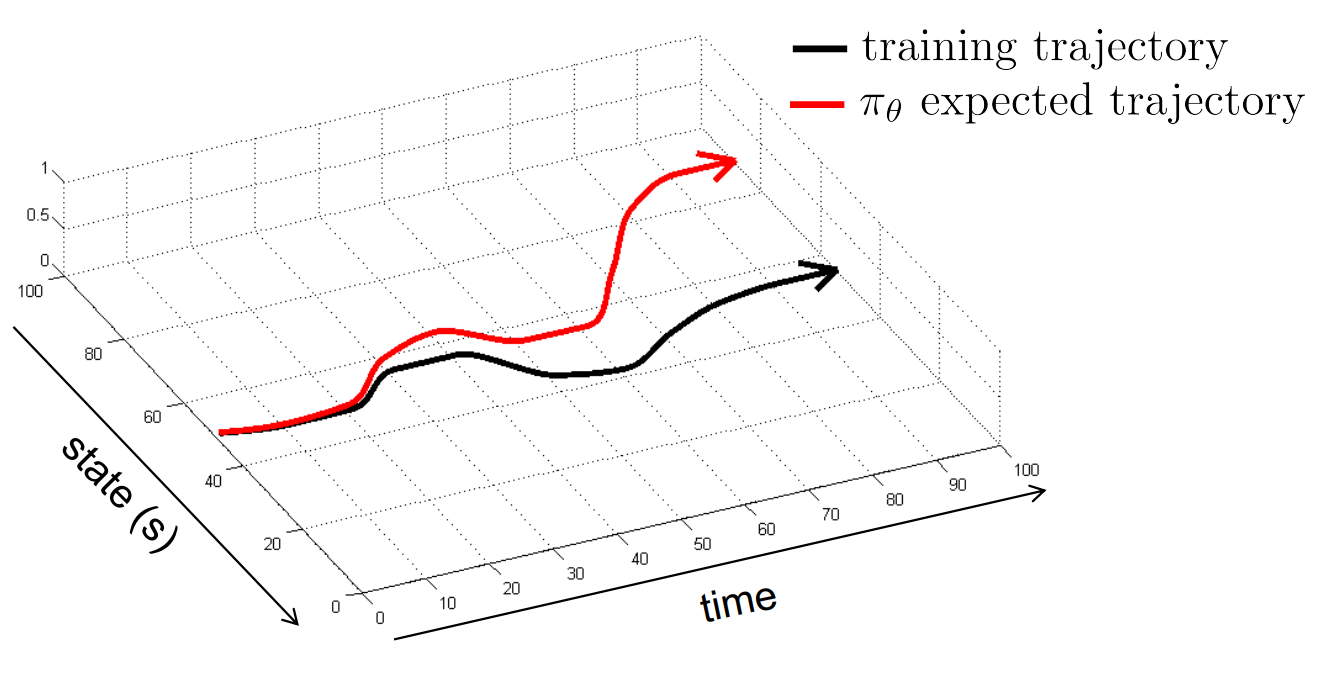
간단한 예시를 들면 우리가 behavior cloning을 사용해서 어떤 policy를 학습한다고 해보자. 이 기법은 이름에 나와있는 것처럼 어떤 policy를 그대로 복사해서 그대로 환경에 올리는 방식인데, 보통은 전문가 데이터를 많이 활용한다. 그런데 만약 policy 내에 stochastic한 속성이 있어, 정해진 state에서 취해야 할 action이 아닌 다른 action을 취했다고 가정해보자. 그러면 그 action을 취했을때의 next_state는 training시 봤던 state가 아닌 다른 state가 나타날 것이고, 이때 error가 생기는데, 문제는 시간이 계속 진행되면서 이 error가 누적되어 최종적으로 학습되었을때 얻는 최종 trajectory와 우리가 바라는 trajectory가 다른 현상이 나타나는 것이다. 만약 feedback이 있었다면 이 error가 발생했을때 이를 보정하기 위해서 다른 action을 취했겠지만 offline 설정에서는 이 feedback 효과를 누릴 수 없다.
또한 overfitting 문제가 나타날 수 있다. 만약 dataset의 크기가 충분하지 않고, 동일 data에 대해서 반복적으로 학습하게 된다면 overfitting이 발생할 수 있다는 것은 잘 알고 있을텐데, 이는 offline 설정에서도 확인할 수 있다.

위의 결과는 HalfCheetah-v2 환경에서 offline 데이터의 크기를 바꿔보면서 학습을 시켰을때의 average reward pattern을 나타낸 것인데, data size를 증가시켜도 reward가 증가하는 경향이 나타나지 않는다. 그런데 재미있는 것은 학습된 Q value를 출력해보면 dataset의 크기에 변화가 있는 경우, Q value에도 변화가 발생하는데, 주목할 부분은 y축의 단위가 log scale이라는 것이다. 즉 1000개의 data를 사용하면 1000번 학습을 했을 때의 Q value는 \(10^{20}\)라는 어마어마한 값을 가지는 것이다, 그런데 이때의 average reward는 -250이다. 즉 학습이 잘 되었어도 실제 성능이 그대로 반영되지 않는 overestimation 문제가 발생하는 것이라고도 볼 수 있는 것이다.
또 다른 문제는 offline 학습시 사용되는 데이터가 환경을 대변할만큼 좋은 데이터가 아닐 수도 있다는 점이다. 하지만 behavior cloning을 하게 되면 그 중에서도 좋은 데이터만을 추출해서 학습시킬 수 있으므로 크게 고려할만한 점은 아니다.
Distribution Shift in a nutshell
사실 문제는 앞에서 언급한 Overfitting이나 bad data 문제보다는 Distribution shift 라는 것에서 파생된다. 만약 지도 학습에서 흔히 볼 수 있는 문제인 Empirical Risk Minimization (ERM)에서는 \(f_{\theta}(x)\)와 \(y\)의 차이를 최소화하도록 \(\theta\)를 찾게 되어있다.
$$ \theta \leftarrow \arg \min_{\theta} \mathbb{E}_{x \sim p(x), y \sim p(y \vert x)}\big[ (f_{\theta}(x) - y)^2 \big] $$
그러면 과연 어떤 지점 \(x^{*}\)에서의 값 \(f_{\theta}(x^*)\)은 항상 맞는 값을 가질까? 만약 학습시 overfitting이 발생하지 않았다면 위 식의 expectation term (\(\mathbb{E}_{x \sim p(x), y \sim p(y \vert x)}\big[ f_{\theta}(x) - y)^2 \big]\))은 작은 값을 가질 것이다. 당연히 잘 학습이 되었다면 동일한 distribution에서 뽑은 새로운 샘플을 넣었을때도 이에 대한 expectation이 작게 된다. 그런데 offline 설정처럼 다른 distribution에서 샘플을 뽑게 되면 이 값은 작다고 할 수 없다.
$$ \mathbb{E}_{x \sim \bar{p}(x), y \sim p(y \vert x)}\big[ (f_{\theta}(x) - y)^2 \big] \quad \text{ for general } \bar{p}(x) \neq p(x) $$
그렇다고 하더라도 \(x^*\)를 \(p(x)\)에서 샘플링하는 것도 offline 설정에서는 \(p(x)\)에 대해서 알 수 없기 때문에 할수가 없다.
그런데 사실 보통 value network 등을 사용할 때 신경망을 사용하게 되는데, 이 신경망은 데이터만 많으면 generalize가 잘 되기 때문에 크게 신경쓸 필요는 없다.
그러면 이런 케이스는 어떨까? 만약 \(x^*\)를 다음과 같이 구하면 어떻게 될까?
$$ x^* \leftarrow \arg \max_x f_{\theta}(x) $$

위의 그래프는 학습된 함수 \(f_{\theta}(x)\)와 \(y\)와의 비교를 나타낸 함수인데, 파란색이 학습된 함수, 초록색이 \(y\)라고 했을 때 만약 어떤 \(x\)를 \(\arg \max_{x} f_{\theta}(x)\)로 뽑는다면 아이러니하게도 해당 지점은 \(y\)와의 차이가 제일 큰 지점이 된다. 결과적으로 신경망이 generalization을 아무리 잘 했다고 하더라도, optimization 과정을 통해서 적절한 값을 구하는 것은 또다른 문제가 된다는 것을 의미한다.
Where do we suffer from distribution shift?
그러면 강화학습에서는 distribution shift에 의해서 영향을 받는 부분이 어떤 것일까? 우선 bellman equation을 보되, 일단 actor-critic 구조의 bellman error를 살펴본다.
$$ Q(s, a) \leftarrow \underbrace{r(s, a) + \mathbb{E}_{a' \sim \pi_{new}}[Q(s', a')]}_{y(s, a)} $$
그러면 일반적인 bellman equation 의 Q value를 구하는 때 \(\max\)를 취하는 것과 다르게 새로운 policy \(\pi_{new}\)에 의해 뽑인 action을 취했을때 Q value의 평균을 사용하게 되고, 여기에 해당 state와 action에서 받은 reward를 합쳐 앞에서 언급한 \(y\)라고 볼 수 있다. 그러면 강화학습에서의 objective는 다음과 같이 정의할 수 있다.
$$ \min_{Q} \mathbb{E}_{(s, a) \sim \pi_{\beta}(s, a)} \big[(Q(s, a) - y(s, a))^2\big] $$
여기서 expectation을 취하는 \((s, a)\)는 behavior policy \(\pi_{\beta}\)에서 나오는 것이고, target value인 \(y(s, a)\)는 behavior policy가 아닌 다른 policy ( bellman equation에서는 \(\pi_{new}\)를 사용했다)로 계산된 것이다. 당연히 잘 학습이 되었다면 \(\pi_{\beta}(a \vert s) = \pi_{new}(a \vert s)\)일때 좋은 성능을 보여줄 것이다. 그런데 이전 distribution shift의 문제에서 언급했던 것처럼 \(\pi_{new}\)를 \(\arg \max_{\pi} \mathbb{E}_{a \sim \pi (a \vert s)} [Q(s, a)] \)로 정의한다면 좋은 성능을 기대하기 어려워진다. 그래서 그림 6에서 본 것과 같이 dataset을 더 넣고 학습을 더한다고 해서 실제값과의 error는 더 커질 가능성이 생기기 때문이다.
Where else do we suffer from distribution shift?
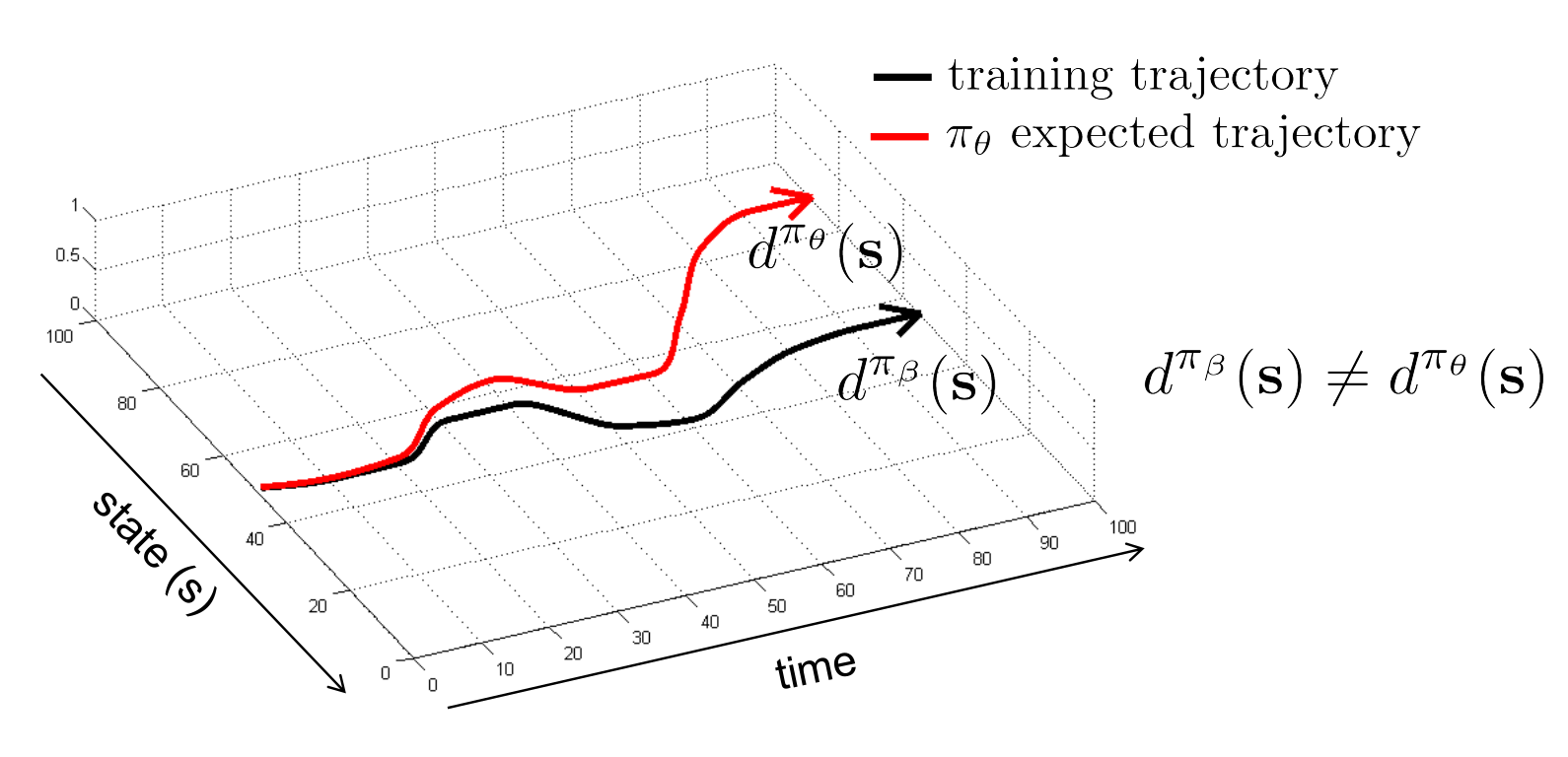
물론 앞에서 언급한 것처럼 offline 설정 상에서 학습된 policy와 평가받는 policy의 distribution이 다르면, 학습하는 \(\pi_{\theta}\)가 fixed dataset에서 잘 학습되었더라도, 실제 control시 사용할 \(\pi_{\beta}\)는 성능이 안 좋을 수 있다.
Sampling & function approximation error
그리고 당연히 Sampling 데이터의 오류에 의해서 value function approximation error도 존재한다.
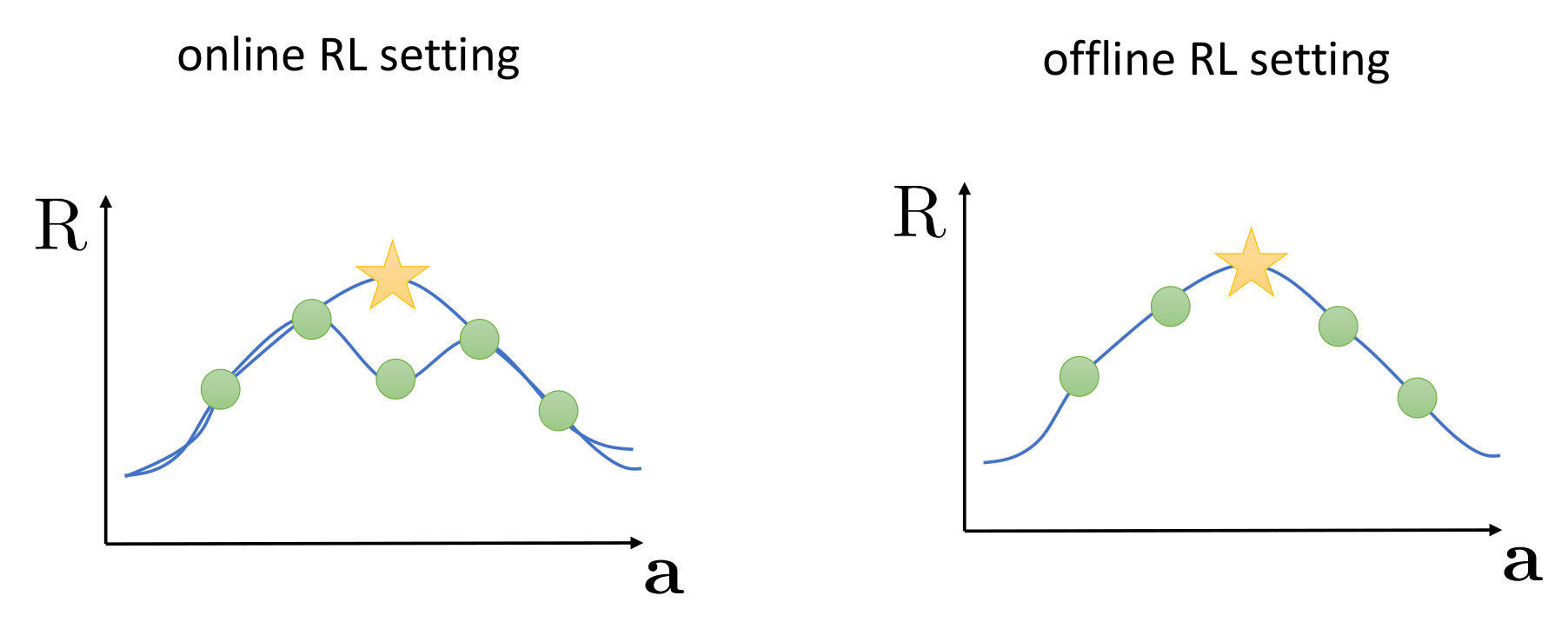
보통 dataset을 통해서 정확한 value function을 묘사한다기 보다는 이 value function에 어느 정도 근사하는 approximation 이 활용된다. 그렇기 때문에 많이 직접 가지고 있지 않은 데이터라도 주변 데이터를 통해서 유추할 수 있는데, 만약 잘못 샘플링된 데이터(가운데 초록색 점)가 있을때 online같은 경우는 이를 추정값(별)과 비교해서 이를 value function에 반영할 수 있기 때문에 policy를 개선할 수 있지만, offline 설정에서는 이런 과정 자체가 아예 불가능하다. 결국 그냥 추정값 그대로 value function approximation을 수행하게 되고, 일반적인 RL에서 발생하는 sampling error나 function approximation error는 offline 설정에서는 조금 더 크게 부각될 수 있다.
Offline RL with Policy Gradient
서두에서 언급했던 것처럼 Offline RL은 과거에는 Batch RL이라는 이름으로 연구가 되어 있었고, 여러 시도 중에는 Policy Gradient에 Offline RL을 적용한 케이스가 있다. 일반적인 강화학습의 목표는 다음과 같이
$$ \max_{\pi} \sum_{t=0}^T \mathbb{E}_{s_t \sim d^{\pi}(s), a_t \sim \pi(a \vert s)} [\gamma^t r(s_t, a_t)] $$
total expected reward를 최대화하는 것인데, 이 때 policy gradient를 취해보면 다음과 같다.
$$ \begin{align} \nabla_{\theta} J(\theta) &= \mathbb{E}_{\tau \sim \pi_{\theta}(\tau)} \big[ \sum \nabla_{\theta} \gamma^t \log \pi_{\theta} (a_t \vert s_t) \hat{Q}(s_t , a_t) \big] \\ &\approx \sum_{i=1}^{N} \sum_{t=0}^T \nabla_{\theta} \gamma^t \log \pi_{\theta} (a_{t, i} \vert s_{t, i}) \hat{Q}(s_{t, i}, a_{t, i}) \end{align} $$
이 모든 과정을 하기 위해서는 결국 \(\pi_{\theta}\)에서 뽑은 샘플 데이터가 있어야 하는데, offline 설정을 적용해보면 현재는 \(\pi_{\theta}\)가 아닌, \(\pi_{\beta}\)가 있는 셈인 것이다. off policy 설정에서는 이렇게 서로 샘플링에 대한 분포 차이를 해소하기 위해서 분포의 차이를 가중치로 활용한 importance weight라는 것을 사용했고, 이를 통해 importance sampling을 수행했다. policy gradient에서 importance sampling은 다음과 같이 나타낼 수 있다.
$$ \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \underbrace{\frac{\pi_{\theta}(\tau_i)}{\pi_{\beta}(\tau_i)}}_{\llap{\text{importance}} \rlap{\text{ weight}}} \sum_{t=0}^T \nabla_{\theta} \gamma^t \log \pi_{\theta} (a_{t, i} \vert s_{t, i}) \hat{Q}(s_{t, i} \vert a_{t, i}) $$
이렇게 unbiased하면서 consistent한 estimator를 만들 수 있지만, 대신 high variance를 가지는 단점이 있다.
여기서 importance weight를 정의해보면 다음과 같다
$$ \frac{\pi_{\theta}(\tau)}{\pi_{\beta}(\tau)} = \frac{p(s_1) \prod_t p(s_{t+1} \vert s_t, a_t) \pi_{\theta}(a_t \vert s_t)}{p(s_1) \prod_t p(s_{t+1} \vert s_t, a_t) \pi_{\beta}(a_t \vert s_t)} $$
그런데 잘보면 importance weight의 상당수 term은 중복이 되기 때문에 상쇄시킬 수 있고, 결과적으로는 다음의 항목만 남게 된다.
$$ \frac{\pi_{\theta}(\tau)}{\pi_{\beta}(\tau)} = \frac{\prod_t \pi_{\theta}(a_t \vert s_t)}{\prod_t\pi_{\beta}(a_t \vert s_t)} $$
이렇게 되면 결과적으로 \(\pi_{\beta}\)에 대한 정보 없이는 importance weight를 계산할 수 없다. 그리고 만일 이 정보를 알고 있을지라도 \(\pi\)항이 \(T\)번, 즉 전체 horizon만큼 곱해지는 형태를 띄기 때문에 결과적으로 \(T\)에 대해서 exponential되는 경향이 있는데, \(\pi\) term이 결국은 어떤 확률값을 나타내기 때문에 분모와 분자는 0으로 exponentially decrease하는 형태로 표현될 것이다. 그래서 off-policy에서도 importance weight 속성을 활용한 importance sampling 기법을 사용하긴 하지만, \(T\)가 길어지면 길어질수록 0으로 빠르게 작아지기 때문에, 수치적으로 뭔가를 계산하기에는 적절하지 않다.
그래서 policy gradient에서는 이런 문제를 극복하기 위해서 log-Derivative trick을 사용한다. (아마 다른 강의에서는 grad-log-pi라고 표현되는 곳도 있을테고, 이 내용은 이전에 한번 RL Spinning Up 포스트에서 언급했던 내용이다.) 그리고 이번 섹션인 Offline RL 설정에서의 policy gradient에서는 다음과 같이 정의를 해준다.
$$ \nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^T \Big( \prod_{t'=0}^{t-1} \frac{\pi_{\theta}(a_{t', i} \vert s_{t', i})}{\pi_{\beta}(a_{t', i} \vert s_{t', i})} \Big) \nabla_{\theta} \gamma^t \log \pi_{\theta}(a_{t, i} \vert s_{t, i}) \Big( \prod_{t'=t}^{T} \frac{\pi_{\theta}(a_{t', i} \vert s_{t', i})}{\pi_{\beta}(a_{t', i} \vert s_{t', i})} \Big) \hat{Q}(s_{t, i}, a_{t, i}) $$
식은 복잡하게 표현되어 있지만, 사실 앞에서 다뤘던 \(J(\theta)\)에 대한 미분값 표현은 동일하다. 다만 합을 구하는 구간이 \(t=0\)에서 \(t-1\)까지, 그리고 \(t\)부터 \(T\)까지로 두 부분으로 나눠진것이다.(어차피 곱셈이기 때문에 저렇게 두 부분으로 나눠도 크게 상관이 없다.)
이 두 부분이 하는 역할이 조금씩 다르다. 첫번째 부분에서는 우리가 학습할 policy \(\pi_{\theta}\)가 dataset에 정의된 policy \(\pi_{\beta}\)와 다른 정도에 대한 importance weight다. 대신 \(t-1\), 즉 과거의 데이터에 대해서 현재 학습할 policy와 behavior policy간의 차이를 나타내는 값이 된다. 결과적으로 첫번째 부분을 통해서는 \(\pi_{\theta}\)가 action을 취했을 때 \(s_t\)에 도달할 수 있는지에 대한 추정값을 나타낸 것이다.
두번째 부분은 \(\hat{Q}\), 즉 dataset의 \(\pi_{\beta}\)로부터 추정한 Q value를 가지고 있을때 \(t\)부터 \(T\)까지의 importance weight를 계산한 것이다. 이 값을 통해서 \(\hat{Q}\)가 얼마나 잘 추정하고 있는지를 판단하고, 이를 보정해주는 역할을 수행한다. 다르게 표현하면 첫번째 부분과 다르게 미래의 reward에 대한 보정이랄까?
그런데 여기서 보통 연구할 때 가정을 하는 것은 첫번째 항은 거의 상쇄한다는 점이다. 물론 정확한 것은 아니기에 상쇄할 수 없는 것으로 생각할 수도 있겠지만, 많은 연구들을 통해서 \(pi_{\beta}\)와 \(\pi_{\theta}\)의 lower bound를 계산해보면 거의 비슷한 값을 가지기에 상쇄하는 것을 가정을 둔다.
결국 상쇄되는 term을 배제하고 다시 식을 정리하면 다음과 같이 된다.
$$ \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t'=0}^T \nabla_{\theta} \gamma^t \log \pi_{\theta}(a_{t, i} \vert s_{t, i}) \Big( \prod_{t'=t}^T \frac{\pi_{\theta}(a_{t', i} \vert s_{t', i})}{\pi_{\beta} (a_{t', i} \vert s_{t', i})} \Big) \hat{Q}(s_{t, i}, a_{t, i}) $$
그런데 여기에서 \(\hat{Q}\)는 결국 미래 reward에 대한 expectation이므로 다음과 같이 근사화를 할 수 있다.
$$ \hat{Q}(s_{t, i}, a_{t, i}) = \mathbb{E}_{\pi_\theta} [ \sum_{t'=t}^T \gamma^{t' - t} r_{t'}] \approx \sum_{t'=t}^T \gamma^{t'-t} r_{t', i} $$
그러면 이 값을 앞의 수식에 대입해보면 다음과 같이 식이 나오는데 여기서 production을 취하는 영역과 summation을 취하는 영역이 겹치기 때문에 production에 대한 영역을 \(T\)까지가 아닌 \(t'\)까지로만 한정지어서 계산할 수 있게 된다.
$$ \sum_{t'=t}^T \Big( \prod_{t''=t}^T \frac{\pi_{\theta}(a_{t'', i} \vert s_{t'', i})}{\pi_{\beta}(a_{t'', i} \vert s_{t'', i})} \Big) \gamma^{t'-t} r_{t', i} = \sum_{t'=t}^T \Big( \prod_{t''=t}^{t'} \frac{\pi_{\theta}(a_{t'', i} \vert s_{t'', i})}{\pi_{\beta}(a_{t'', i} \vert s_{t'', i})} \Big) \gamma^{t'-t} r_{t', i}$$
물론 이렇게 하면 앞에서 언급한 것처럼 production의 범위가 한정되어서 연산량이 줄긴 하지만, 여전히 T가 길어지면 길어질수록 0으로 작아지는 현상은 남아있기 때문에 이런 것을 완전히 배제하기 위해서는 importance sampling 기법이 아닌 value funciton을 가지고 추정하는 방법을 사용해야 한다. 다시 말해서 \(Q^{\pi_{\theta}}(s, a)\)를 추정하는 방법 말이다.
이 때 적용해볼 수 있는 방법 중 하나가 Doubly robust estimator(Jiang et al, Doubly robust off-policy evaluation for reinforcement learning, ICML 2016)이다. 물론 importance weight를 쓰는 이상 exponential 현상은 막을 수 없지만, 적어도 high variance 효과를 줄일 수 있는 방법이다. 위의 식에서 \(i\)에 대한 정의를 축약하고, importance weight를 \(\rho\)로 표기하면 다음과 같이 정의할 수 있다.
$$ \begin{aligned} V^{\pi_{\theta}}(s_0) &\approx \sum_{t=0}^T \Big( \prod_{t'=0}^t \rho_{t'} \Big) \gamma^t r_t \\ &= \rho_0 r_0 + \rho_0 \gamma \rho_1 r_1 + \rho_0 \gamma \rho_1 \gamma \rho_2 r_2 + \dots \end{aligned} $$
그러면 뭔가 recursive한 형태를 띄게 되고 이를 잘 정리한 값을 \(\bar{V}^T\)라고 한다. 이때 \(\bar{V}^{T+1-t} = \rho_t ( r_t + \gamma \bar{V}^{T-t}) \)의 관계를 가진다. 여기에다가 doubly robust estimation이라는 것을 사용하는데 원래 이 기법은 어떤 모델의 결과를 결합시켜서 결과에 대한 causal effect를 추정하는 통계 기법 중 하나이다. 이 방식을 강화학습에서 활용하면 value를 다음과 같이 추정할 수 있다.
$$ V_{DR}(s) = \hat{V}(s) + \rho(s, a) (r_{s, a} - \hat{Q}(s, a)) $$
위 식에서 \(\hat{V}\)와 \(\hat{Q}\)은 model이나 value approximator로부터 파생된 것이다. \(\hat{Q}\)은 function approximation을 통해 나온 것이고, \(\hat{V}\)은 학습할 policy \(\pi_{\theta}\)에 대한 expected value가 될 것이다. 그럼 이 결과를 앞에서 정의했던 recursive term에 적용해보면 최종적으로 다음과 같은 관계를 구할 수 있다.
$$ \bar{V}_{DR}^{T + 1 - t} = \hat{V}(s_t) + \rho_t(r_t + \gamma \bar{V}_{DR}^{T-t} - \hat{Q}(s_t, a_t)) $$
또 하나의 방법은 importance sampling의 문제를 직접적으로 tackling해서 marginalize하자는 것이다. 이 방식은 GenDICE (Zhang et al, GenDICE: Generalized Offline Estimation of Stationary Values in ICML 2020)에서 언급된 내용인데, 문제가 되는 importance weight에 대한 production term을 사용하는 것 대신 state와 action에 대한 분포로 추정하자는 아이디어이다. production term을 다음과 같이 대체한다.
$$ \prod_t \frac{\pi_{\theta}(a_t \vert s_t)}{\pi_{\beta}(a_t \vert s_t)} \to w(s, a) = \frac{d^{\pi_\theta}(s, a)}{d^{\pi_{\beta}}(s, a)} $$
이렇게 하면 \(J(\theta)\)는 \(\frac{1}{N} \sum_i w(s_i, a_i) r_i \)로 추정할 수 있어서 importance sampling에서 발생하는 문제를 완화할 수 있다. 그러면 과연 \(w(s, a)\)를 어떨게 구하냐가 앞에서 소개한 논문의 주요 아이디어이다.
$$ d^{\pi_{\beta}}(s', a') w(s', a') = (1 - \gamma) p_0 (s') \pi_{\theta}(a' \vert s') + \gamma \sum_{s, a} \pi_{\theta} (a' \vert s') p(s' \vert s, a) d^{\pi_\beta}(s, a) w(s, a) $$
이 식에서 첫번째 term은 \((s', a')\)에서 시작할 확률을 나타낸 것이고, 두번째 term은 \((s', a')\)로 전이될 확률을 계산한 것이다. 이런 류의 방정식을 푸는 문제를 consistency problem이라고 하는데, 굳이 강화학습 뿐만 아니라 식으로 이뤄진 형태의 문제의 solution을 찾는 문제인데, 식은 복잡하게 쭉 되어 있지만 아이디어는 우리가 학습할 policy \(d^{\pi_\theta}\)를 \(d^{\pi_{\beta}} \times w(s, a) \)로 대체하는 것이다. 이를 통해서 환경에 대한 MDP의 occupancy를 측정할 수 있는 척도를 계산하게 된다. 이 문제는 보통 fixed point problem이라 언급되며, 이를 해결하고자 하는 시도들이 많이 연구되었다.
Offline value function estimation
그럼 offline 설정이 과거에 나오지 않았던 새로운 컨셉인가 싶지만, 앞에서도 언급했다시피 과거에도 batch rl이란 이름으로 연구되어 있던 내용이었다. 그런데 단순하게 approximate dynamic programming과 Q-learning을 그냥 offline 설정으로 수행하겠다는, 개념을 확장시킨 형태였고 일반적으로는 replay buffer의 크기를 크게 해서 해당 데이터를 학습하는 형태로 되어 있었다. 그래서 이를 단순한 function approximator를 사용해서 어느 정도 근접한 solution을 도출하고자 했다.
하지만 연구가 진행되면서 이런 solution을 구하기 위해서는 신경망과 같이 highly expressive function approximator가 필요하다는 것을 알게 되고, 앞에서 언급되었던 offline RL의 문제가 발생하는 요인 중 핵심이 바로 distribution shift라는 것을 확인했다. 기존에는 distribution shift의 관점에서 고려되지 않았기 때문에, 이에 대한 연구가 현재 진행되고 있는 것이 현재의 방향이다.
Modern Offline RL algorithms
(해당 내용은 추후에 추가할 예정)
Off-Policy Evaluation and Model Selection
보통 강화학습의 문제는 총 보상이 최대가 될 수 있는 좋은 policy를 찾는 것이지만, Offline RL에서는 물론 좋은 정책을 찾는 것도 중요하지만 환경 상에서 해당 policy를 수행하지 않고도, 주어진 policy의 좋은 정도를 판단할 수 있느냐는 것이다. 예를 들어서 어떤 behavior policy \(\pi_{\beta}\)가 수행되고 있을때의 dataset을 바탕으로 value function \(V^{\pi_{\beta}}(s)\)가 나온다면, 이 policy의 value가 다른 policy의 value (예를 들어서 \(V^{\pi_\theta}\))보다 좋은 것을 어떻게 알 수 있을까? 이를 위해서 Offline RL에서 필요한 과정 중 하나가 Off-policy Evaluation (OPE)이다. 간단하게 behavior policy와 target policy간의 평가에 대한 내용이다. Offline RL은 이 OPE를 통해서 Model selection을 하게 되는데, 보통 특정 policy를 찾거나 policy에 최적화된 hyperparameter를 찾는 과정을 하게 된다.
아마 인공지능을 공부한 사람이라면 위에서 소개한 일련의 과정을 많이 봐왔을텐데 바로 supervised learning에서이다. supervised learning에서도 어떤 dataset에서 샘플링을 한 데이터를 바탕으로 학습하고, 어떤 hyperparamter의 조합으로 최적의 모델을 찾는데, 그 과정에서 겪는 문제를 동일하게 겪는다고 보면 된다. 예를 들어서 overfitting이 발생할 수도 있고, underfitting이 발생할 수도 있고... 그렇다고 이 hyperparamter를 찾는 명확한 방법론이 나온 것도 아니다.
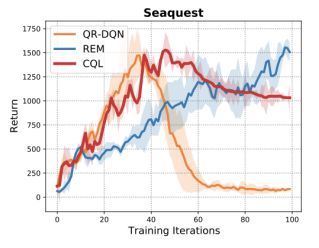
위의 그래프는 Atari에 있는 게임 중 Seaquest라는 게임에서의 Offline RL algorithm(QR-DQN, REM, CQL) 간의 성능을 비교한 것이다. 이 결과를 봤을 때도 어떤 알고리즘 모델이 좋은지를 판단할 수 없다. 또한 특정 알고리즘을 선정했을때도 최적의 성능을 보이는 training iteration (epoch) 값도 제각기 다르다. 예를 들어서 CQL 같은 경우는 epoch이 50인 모델이 더 학습시킬수록 overfitting 현상이 나타나기도 하고 REM은 학습을 시키면 시킬수록 성능이 좋아지는 경향이 나타나기도 한다. 결론적으로는 이 hyperparameter를 찾는 방법을 찾아야 하는데, supervised learning처럼 early stopping을 써서 개선하는 방법도 있을 수 있고, 적용해볼 가능성은 다양하다.
(OPE 방법론에 대한 내용은 추후 업데이트)
How should we evaluate offline RL methods?
서두에서도 언급했던 것처럼 Offline RL은 다음과 같은 상황에서 도움을 받을 수 있다.
- good behavior와 bad behavior로 가득차있는 dataset 상에서 좋은 점을 찾는 법
- (가정이긴 하지만) 특정 영역에서의 good behavior가 다른 영역에서도 잘 동작할 것이라는 점에서의 Generalization
- good behavior들의 조합을 통해서 최적의 정책을 찾는 법 (Stitiching)
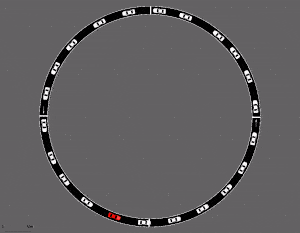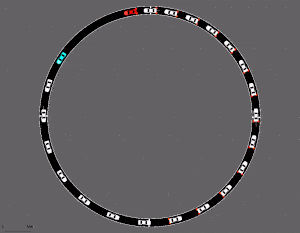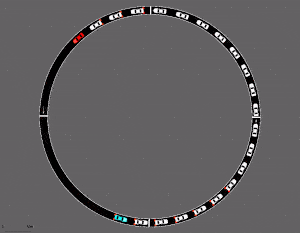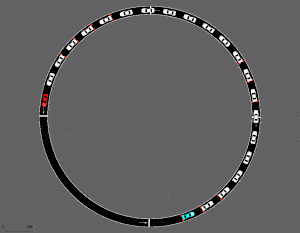
여기서 Stitiching에 대해서 부연 설명을 하자면 미로 찾기 학습을 들 수 있다.
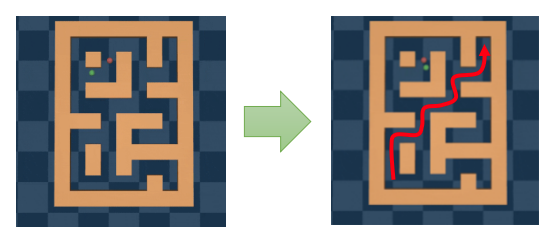
물론 강화학습을 길찾기를 적용해볼 수 있는 부분은 다양하지만 offline RL 설정으로 한정을 해보자면, 정해진 영역에서의 goal까지의 길을 탐색하는 방법을 dataset을 통해 학습하게 되면 이 경험의 조합을 바탕으로 최종 goal까지의 경로를 찾을 수 있게 된다. (참고로 위의 예시는 Offline RL dataset인 D4RL에서 제공되는 maze2d 환경인데, 초록색 공이 agent, 빨간색 공이 target이고, 초록색 공이 빨간색 공에 도달했을 때 보상을 받는 형태로 되어 있다.)
그러면 단순히 좋은 데이터만 찾아서 그 행동을 따라하게 하면(마치 behavior cloning처럼) 결국 좋은 policy가 아닌가 의문을 가질 수도 있다. 그런데 보통 이런 강화학습을 적용해야하는 실제 사례는 보통 stochastic한 환경이 많다. 이 말은 특정 state에서 어떤 action을 취했을때 과연 이 action이 정말 좋은 행동인지는 판단할 수 없다는 것을 의미하는 것이다. 어떤 policy가 action을 취했어도 이에 대한 reaction이 환경에 의해서 발생한 것인지, 아니면 확률에 따라 우연하게 발생한 것이지 모르기 때문이다. 그래서 단순히 좋은 action을 관찰한 것만 가지고 좋은 policy를 찾는 것은 쉬운 일이 아니다.
How do we know if it's going to work?
그러면 Offline RL의 가장 큰 문제는 과연 policy를 실제로 돌려보지도 않고 어떻게 잘 동작하는지를 판단하냐는 것이다. 사실 이 문제가 Offline RL이 실제로 적용되는게 어려운 큰 장애물이기도 하다. 그리고 딱히 명확한 solution도 존재하지 않는다. 물론 앞에서 언급한 OPE를 사용하면 "어느정도" 좋은 policy를 찾을 수 있겠지만, 여기에도 hyperparameter search 과정이 필요하다. 그래서 결국 필요한 것은 실제가 아닌 simulator같은 것을 사용해서 평가한다. (그래서 offline RL의 실제 적용케이스는 거의 대부분 simulator가 제공되는 MuJoCo 환경이나 CARLA같은 자율주행 simulator로 한정되어 있다.)
 |
 |
 |
(출처: D4RL)
How do we evaluate offline RL methods?

앞에서 썼던 그림을 가져오면 offline RL에 사용할 policy가 어떤 것이던간에 해당 policy가 수행한 trajectory를 dataset화해서 해당 데이터를 학습하는 형태로 되어 있다. 그러면 가장 간단하게 생각해볼 수 있는 것은 그냥 online RL을 수행한 결과를 바탕으로 학습시키는 것이다. 일반적으로는 이런 과정을 가질 것이다.
- online RL을 사용해서 \(\pi_\beta\)를 학습한다
- training 과정에서 발생된 data를 수집한다 or 학습이 완료된 \(\pi_\beta\)를 사용해서 data를 수집한다.
그런데 사실 이 방법은 그렇게 좋지 않은 방법이다. 실제 환경에 적용하기 위해서는 data가 non-markovian property를 가지는 policy로부터 data를 가져와야 한다. 예를 들어서 사람이 직접 데이터를 수집한다던가, 아니면 직접 수정한 policy를 가지고 데이터를 수집해야 하는 것이다. 아무래도 학습이 다되거나 진행중인 policy를 바탕으로 데이터를 수집할 경우 현실 환경의 dynamic를 대표할 수 있는 대표성이 떨어지게 되고(아무래도 exploration case가 적어지는 그런 문제가 아닐까 싶다) policy improvement 을 수행할 수 있는 가능성이 줄어들게 되는 것이다. 그래서 적어도 offline RL에서 학습할 데이터는 현실 환경의 설정을 대표할 수 있어야 하고, 개선의 여지가 남아있는 환경이어야 한다. 그래야 offline RL은 behavior policy보다 더 잘 동작하는 policy를 학습할 가능성이 생긴다. 이때문에 이런 가능성에 대한 검증 없이는 offline RL 알고리즘이 잘 동작하는지를 확신할 수 없다.
D4RL: Datasets for Data-Driven Deep RL
그래서 Levine 교수 랩에서 만든 offline RL용 Benchmark dataset이 D4RL(Datasets for Data-Driven Deep RL)이다. (해당 dataset은 tensorflow datasets 에도 포함되어 있어 만약 tensorflow로 개발한다면 도움을 받을 수 있다.) 이 dataset이 바로 앞에서 언급한 그런 속성들을 만족하고 있다.
D4RL
A collection of benchmarks and datasets for offline reinforcement learning
sites.google.com
- Data from non-RL policies - RL이 개입하지 않은 simulator와 사람이 수집한 데이터를 바탕으로 생성되었다.
- Stitching - 앞에서 잠깐 소개한 2D maze가 그런 문제인데, 어떻게 보면 Dynamic Programming으로도 좋은 solution을 찾을 수 있다. 그래서 dataset을 통해서 개선할 여지를 어느정도 만들어둔 것이다.
- Realistic Task - 기존의 gym이나 MuJoCo 환경이 아닌, 조금더 현실적인 dataset들도 포함되어 있다. 예를 들어서 앞에서 잠깐 보여준 CARLA simulator나 Kitchen 환경에서 robot manipulation하는 것, 또 Flow simulator에서 Traffic control하는 환경에 대한 offline dataset을 제공한다.
Other properties that are important
이밖에도 Offline RL dataset에 갖춰야 할 중요한 속성들이 더 있다. 물론 D4RL이 상당수 만족하긴하지만 만족시키지 못한 부분들도 존재한다.
- Stochasticity - Offline RL을 어떤 분야에도 적용하고 싶어하지만, 사실 위험성때문에 적용하지 못하는 경제나 의료, 교육 분야에서는 뭔가 구체적으로 표현하지 못하는 확률성을 담고 있기 때문에 이에 대한 benchmark도 없는 편이다. 물론 이런 부분이 만족된다면 해당 분야의 발전은 물론 이런 인공지능 모델도 고도화되지 않을까 싶다.
- Non-stationarity - 그리고 실제 환경은 거의 대부분 시간에 따라서 변화하는 양상을 띈다. 즉, 완전히 동일한 state가 없고, 시간에 따라 변화하는 속성을 현실 환경에서는 발견할 수 있는 속성이다. (보통 비정상성이라고 표현하기도 한다.)
- "Risky" dataset biases - dataset내에 어느정도의 bias가 존재하는 것을 고려해야 한다. 예를 들어서 offline RL로 자율주행 agent를 개발할때 만약 해당 dataset내에 사고가 난 것에 대한 data가 없다면, 해당 agent는 사고가 나는 것을 피할 수 있을까? 물론 이에 대한 dataset을 쌓는 것도 힘든 부분이지만, 반드시 고려해야 할 속성이기도 하다.
- Partial Observability - 당연한 이야기이겠지만 신이 아닌 이상 현실 세계에서 모든 state를 관찰할 수 없다는 점도 고려되어야 한다. 이 부분은 tutorial에서 다뤄지지 않았지만, 중요한 속성 중 하나이다.
Open Problem
Over-Conservatism?
앞에서 소개한 알고리즘이나 접근 방식 모두 기존의 behavior policy에서 크게 벗어나지 않는 범위내에서 action을 취하는 것을 다루고 있지만(이를 over-conservatism, 과도하게 보전적으로 action을 취하는 형태라고 표현하는 것 같다..) 사실 학습이 잘되고, 환경에 대한 generalization이 잘 이뤄진다면 굳이 이런 방향으로 나아가지 않아도 된다. 이런 측면에서 알고리즘 영역에서 다뤘던 Uncertainty 기반의 방법론이 generalization에 대한 tradeoff를 고려하면서 사용할 수 있다.

물론 이를 위해서는 당연히 uncertainty를 추정하는 방법이나, 이를 보정하는 방법에 대해서도 고민해야 한다.
Hyperparameter Tuning
앞에서 언급했던 것처럼 OPE에서는 policy의 성능을 좌우할 hyperparameter가 있을텐데, 이를 tuning하기 위한 general한 OPE가 필요할 것인가에 대한 문제도 존재한다. 아니면 training시 supervised learning처럼 "validation error"에 따라서 최적화를 수행하는 것도 있을 수도 있고, 혹은 OPE 과정 중 특정 policy에 대해서 평가할 수 있느냐에 대한 문제들이 존재한다.
한가지 아이디어는 굳이 policy의 return이나 value function을 학습하지 않고, policy간의 순위를 매기는 것에 초점을 맞추자는 것이다. (Paine, Paduaru et al. Hyperparameter Selection for offline reinforcement learning, offline RL workshop in NeurIPS 2020) 이 논문에서는 Rank Correlation이라는 것을 사용해서 OPE내의 policy 중 우선 순위를 찾는 것을 소개했다.
$$ \text{Regret @ 1} = \max_{\pi \in \Pi} J(\pi) - J \Big( \arg \max_{\pi \in \Pi} \hat{J}(\pi)\Big) $$
Function approximation

사실 Offline RL에서 신경망을 사용하는 이유는 아마도 신경망이 제공하는 generalization effect를 통해 function approximation을 하기 위함일 것이다. 하지만 특히 offline 설정의 경우는 주어진 data가 한정적일뿐더러 오차를 보정할 새로운 데이터가 제공되지 않기 때문에, 이 경우 function approximation은 성능은 급격하게 안 좋아진다. 예를 들어서 supervised learning에서도 주어진 데이터만 가지고 학습하고, 동일한 데이터로 반복적으로 학습할 경우 overfitting이 발생한다던지 성능에 좋은 영향을 주지 않는다. 이 경우 최적화가 정상적으로 이뤄지지 않는다거나 generalization이 잘 안되는 문제가 생기는 것인데, 이 문제는 다양한 방법을 시도해볼 수 있다. 예를 들어서 Representation learning을 한다던가 Causal inference를 사용하거나, 아니면 아예 신경망 구조를 바꿔서 function approximation을 다르게 해볼 수 있게한다던지 말이다.
여기까지가 Tutorial에서 언급한 내용을 간단하게 요약한 것이다. 개인적으로는 물론 최근에 meta RL이나 Modular RL과 같이 다양한RL 연구주제들이 연구되고 있지만, Offline RL 주제 자체는 그 목적이 환경과 interaction이 이뤄지면 학습이 되는 RL의 한계를 넘어서려는 시도가 아닐까 해서 관심있게 보고 있다. 어떻게 보면 강화학습이면서 다른 관점에서는 supervised learning의 측면도 보이고, 혹은 hyperparameter tuning 측면에서도 볼 수 있기 때문에 점점 주제가 섞이는 과정 중 하나인 듯 하다. 물론 그렇다고 내가 잘하는 것은 아니지만, 그래도 현업에서 이 기술을 적용하고자 시도하는 입장에서 한번 내용을 정리해보았다. 부족한 내용은 추후에 더 보충할 예정이다.
'Study > AI' 카테고리의 다른 글
| [RL] CS285 - Policy Gradients (0) | 2022.11.09 |
|---|---|
| [RL][Review] Deterministic Policy Gradient Algorithm (3) | 2022.11.03 |
| [RL][Review] Hyperparameter Selection for Offline Reinforcement Learning (0) | 2022.05.19 |
| [RL][Review] Offline RL without Off-Policy Evaluation (onestep-rl) (0) | 2022.04.19 |
| [RL][Review] Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction (BEAR) (0) | 2022.04.13 |
| [RL][Review] Off-Policy Deep Reinforcement Learning without Exploration (BCQ) (2) | 2022.04.12 |
| [RL] Offline (batch) Reinforcement Learning의 의미와 적용 (2) | 2022.03.18 |
- Total
- Today
- Yesterday
- Offline RL
- 인공지능
- Pipeline
- 파이썬
- Kinect for windows
- End-To-End
- Kinect SDK
- Policy Gradient
- Expression Blend 4
- DepthStream
- Off-policy
- Variance
- Distribution
- reward
- ColorStream
- TensorFlow Lite
- 딥러닝
- RL
- Gan
- Kinect
- bias
- SketchFlow
- PowerPoint
- 한빛미디어
- windows 8
- arduino
- processing
- Windows Phone 7
- dynamic programming
- 강화학습
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
