티스토리 뷰
(해당 포스트는 UC Berkeley 에서 진행된 CS285: Deep Reinforcement Learning, Decision Making and Control를 요약한 내용이며, 그림들은 강의 장표에서 발췌한 내용입니다.)
CS 285
GSI Yuqing Du yuqing_du@berkeley.edu Office Hours: Wednesday 10:30-11:30am (BWW 1206)
rail.eecs.berkeley.edu
Comparison to maximum likelihood
이전 포스트의 마지막에 다뤘던 식이 아래와 같다.
$$ \nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \big( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i, t} \vert s_{i, t}) \big) \big(\sum_{t=1}^T r(s_{i, t}, a_{i, t})\big) $$
그러면 위 식에서 수 식을 통해서 도출한 \(\nabla_{\theta} \log \pi_{\theta} (a_{i, t} \vert s_{i, t})\)가 어떤 의미를 가지고 있을까? \(\pi_{\theta}\)는 말 그대로 특정 state에서 특정 action을 취할 확률을 나타내는 것이고, \(\log \pi_{\theta}\)는 결국 log probability를 구하는 형태가 된다. 그래서 결과적으로 여기에 gradient를 취한것이 될텐데, 쉽게 말해서 신경망이 어떤 policy를 가지고 있을 때 output이 log를 취한 형태가 나오고, 그러면 이때의 derivative를 바탕으로 신경망을 update하는 것이다. 보통 supervised learning을 하게 되면 취할 수 있는 방법 중 하나가 Maximum Likelihood가 있는데, 이때 log probability를 maximize하는 형태로 진행되는데, 이때의 cost function을 보면 policy gradient와 유사한 부분이 있다.
$$ \begin{aligned} &\text{policy gradient: } \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \big(\sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i, t} \vert s_{i, t}) \big) \big( \sum_{t=1}^T r(s_{i, t}, a_{i, t})\big) \\
&\text{maximum likelihood: } \nabla_{\theta} J_{ML}(\theta) \approx \frac{1}{N} \sum_{i=1}^N \big( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i, t} \vert s_{i, t}) \big) \end{aligned} $$
아마 이전 강의 중 Imitation learning을 본 사람이라면 알겠지만, Imitation learning이 딱 supervised learning처럼 maximum likelihood 방식으로 학습하는 것이다. 아래의 그림이 Policy Gradient와 Maximum likelihood로 gradient를 구하는 방식의 차이를 나타낸 것인데, Policy Gradient는 state와 action로 policy의 parameter \(\theta\)를 학습하는 방면, Maximum likelihood에서는 state, action에 대한 pair를 일종의 학습 데이터로 쌓아놓은 상태에서 그걸 가지고 supervised learning을 하는 것이다. 그래서 앞의 수식 비교에서도 명확하게 차이가 존재하는 부분은 rollout된 reward의 총합이 cost function을 계산할때 고려가 되냐 여부에 따르는 것이다.

사실 이 부분이 가장 중요한 요소인데, 막연하게 maximum likelihood처럼 gradient를 계산하게 되면 어떤 state에서 어떤 action을 취했는지와는 상관없이 grad-log-pi term이 작아지는 방향으로 학습이 되는 반면, policy gradient는 reward sum에 따라서, 즉 좋은 trajectory냐 나쁜 trajectory냐에 따라서 gradient의 update방향이 달라지게 된다. 예를 들어서 나쁜 trajectory여서 reward sum이 negative라면 해당 trajectory는 덜 하는 방향으로, 반대로 좋은 trajectory여서 reward sum이 positive라면 해당 trajectory에 나와있는 대로 선호하게 학습이 된다는 것이다. 결과적으로 요약하자면 policy gradient는 reward sum이 weighted되어 있는 maximum likelihood 방식이라고 할 수 있겠다. 또 이런 특성은 PyTorch와 같이 auto-grad를 제공하는 tool에서는 유용하게 써먹을 수 있다.
Example: Gaussian policy
Policy gradient를 통해 humanoid robot을 걷게끔 policy를 학습하는 예제를 다뤄보면, 이때의 policy는 어떤 continuous 값을 가지는 action을 output으로 내보내는 형태로 되어 있다. 만약 우리가 학습해야 할 policy \(\pi\)의 형태를 아래와 같다고 가정해보자.
$$ \pi_{\theta}(a_t \vert s_t) = \mathcal{N}(f_{NN}(s_t); \Sigma) $$
그래서 policy의 output은 신경망에 \(s_t\)를 넣었을때 나오는 값을 평균으로 하고 \(\Sigma\)를 분산으로 하는 multivariate normal distribution, 혹은 gaussian distribution이라고 하는 distribution의 형태로 나온다. 이때 policy gradient를 하기 위해서는 맨 처음으로 해야 될 것이 policy term에 \(\log\)를 취하는 것이다.
$$ \log \pi_{\theta}(a_t \vert s_t ) = - \frac{1}{2} \Vert f_{NN}(s_t) - a_t \Vert_{\Sigma}^2 + \text{const} $$
여기에 \(\theta\)에 관해서 미분을 취하면 아래의 식으로 나오게 된다.
$$ \nabla_{\theta} \log \pi_{\theta} (a_t \vert s_t) = - \frac{1}{2} \Sigma^{-1} (f_{NN}(s_t) - a_t) \frac{df}{d\theta} $$
(식이 복잡한데, 아마 normal distribution의 log-likelihood 부분을 찾아보면 위의 식이 나와있을 것이다.)
What did we just do?
그러면 이전 포스트에서 다룬 REINFORCE 알고리즘을 다시 가져와보자.
- \(\pi_{\theta}(a_t \vert s_t)\)를 수행해서 trajectory \(\tau^i\)를 샘플링한다.
- \(\nabla_{\theta} J(\theta) \approx \sum_i ( \sum_t \nabla_{\theta} \log \pi_{\theta} (a_t^i \vert s_t^i)) (\sum_t r(s_t^i, a_t^i)) \)
- \(\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta) \)
이전 과정을 통해서 grad-log-pi term을 구했으니까, 이제 위 알고리즘의 두번째를 계산할 수 있다. reward sum이야 실제로 policy를 수행하면서 얻은 reward를 넣으면 된다. 결국 state action pair를 trajectory \(tau\)로 표현하면 아래와 같은 식으로 정리된다.
$$ \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \log \pi_{\theta}(\tau_i) r(\tau_i) $$
그러면 학습이 진행되면 될수록 good trajectory에서 수행된 action은 점점 자주하게 되고, bad trajectory에서 수행된 action은 덜 하게 되는 경향을 띄게 될 것이다. 이는 단순히 주어진 sample trajectory에 대해서 모두 학습하는 maximum likelihood 방식과는 다르며, 어떻게 보면 강화학습의 큰 맥락인 "trial-and-error"을 어느정도 형식화한 형태라고 볼 수 있다. 간단히 말해서 시도해보고 좋은 행동은 자주하고, 나쁜 행동은 덜 하는 방향으로 학습된다고 보면 되겠다.
Partial observability

아마 이전 포스트에서 처음에 작성한 내용을 기억할지 모르겠지만, 전제로 둔 조건중에 policy가 모든 state에 대해서 관찰이 가능하다는 것이 있었고, 이때문에 모든 수식에 state \(s_t\)를 사용했다. 그런데 real world problem이나 대부분의 강화학습 문제는 이 state \(s_t\)가 아닌 observation \(o_t\)를 사용하는 형태로 되어 있다. 즉, 모든 정보가 아닌 일부분의 정보만 가지고 action을 추론해야 하는 것이다. 뭔 차이냐고 생각할 수도 있겠지만, 가장 큰 차이는 observation의 경우 state처럼 markov property를 만족하지 않을 수 있다는 것이다. markov property라고 하면 현재 state는 과거 state의 영향을 받지 않는다는 특성인데, observation은 과거의 observation의 영향을 받지 않는다고 단언할 수 없기 때문에 기본적으로 markov property가 성립하지 않는다고 설정한다.
다행인 것은 실제로 policy gradient를 구하는 과정에서 이 markov property를 활용하는 부분이 없다는 것이다. 그래서 기존의 \(s_t\)를 사용해서 계산하던 cost function의 gradient는 \(s_t\)를 그대로 \(o_t\)로 바꿔서 사용할 수 있다.
$$ \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \big( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i, t} \vert o_{i, t}) \big) \big( \sum_{t=1}^T r(o_{i, t}, a_{i, t})\big) $$
What is wrong with the policy gradient?
지금까지 policy gradient 알고리즘에 대해서 쭉 설명했지만, 사실 그냥 알고리즘을 바로 학습에 적용하면 잘 동작하지 않는다. 밑의 예시를 한번 살펴보자.
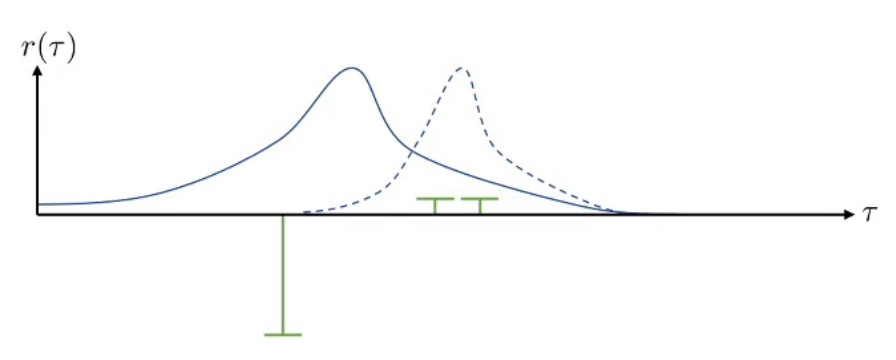
앞에서 언급했던 것처럼 policy gradient는 'trial-and-error' 방식으로 학습하면서 good trajectory를 만든 policy를 자주 수행하고, bad trajectory를 만드는 policy는 덜 수행하는 방향으로 update된다. 참고로 위의 그래프에서 초록색 bar는 해당 trajectory의 reward값 \(r(\tau)\)를 나타낸 것이고, 파란색 curve는 해당 trajectory의 policy인 \(\log\pi_{\theta}(\tau)\), 즉 log probability를 나타낸 것이다. 그러면 negative reward를 받은 trajectory에 대한 log-probability는 낮아지고, positive reward를 받은 trajectory에 대한 2개 샘플의 log-probability는 커질 것이고, 결과적으로 distribution이 점선처럼 이동하게 된다.

그런데 이제는 전체 reward값 자체에 어떤 constant값을 추가해서 위와 같은 경향성을 띈다고 가정해보자. constant를 추가해도 trajectory의 좋고 나쁜 경향성은 유지되고 있으며, 실제로 constant값이 추가되어도 해당 값의 영향은 optimal policy를 구하는 과정에서 max값을 취하면서 없어진다. 그런데 그 경향성이 유지됨에도 불구하고, policy의 distribution이 바로 앞의 그래프보다는 좋은 trajectory를 보이는 policy에 대한 log-probability에 몰리지 않는 성향을 보인다. reward에 offset을 추가했다는 것만으로 이렇게 log-probability 모양이 바뀌는 모습은 이런 policy gradient 방법이 high variance라는 단점을 가지고 있다는 것을 보여주는 것이다. 쉽게 말해서 supervised learning에서 overfit되는 것처럼 학습된 데이터 이외의 unseen data에서는 잘 동작하지 않는 것이다. 이때문에 real world problem에서는 이렇게 policy gradient가 잘 동작하지 않는데, 물론 이를 극복하기 위해 variance를 낮추는 기법이 많이 나와있다.
'Study > AI' 카테고리의 다른 글
| [RL] CS285 - Reducing Variance (0) | 2022.11.09 |
|---|---|
| [RL] CS285 - Off-Policy Policy Gradients (0) | 2022.11.09 |
| [RL] CS285 - Policy Gradients (0) | 2022.11.09 |
| [RL][Review] Deterministic Policy Gradient Algorithm (3) | 2022.11.03 |
| [RL][Review] Hyperparameter Selection for Offline Reinforcement Learning (0) | 2022.05.19 |
| [RL][Review] Offline Reinforcement Learning From Algorithms to Practical Challenges (2) | 2022.04.27 |
| [RL][Review] Offline RL without Off-Policy Evaluation (onestep-rl) (0) | 2022.04.19 |
- Total
- Today
- Yesterday
- processing
- Distribution
- DepthStream
- 파이썬
- Gan
- PowerPoint
- SketchFlow
- windows 8
- Variance
- Expression Blend 4
- Policy Gradient
- reward
- Offline RL
- TensorFlow Lite
- 한빛미디어
- 인공지능
- arduino
- Pipeline
- ColorStream
- Off-policy
- Kinect
- Kinect SDK
- 강화학습
- Kinect for windows
- dynamic programming
- Windows Phone 7
- 딥러닝
- RL
- End-To-End
- bias
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
