티스토리 뷰
(해당 글은 OpenAI Engineer인 Lilian Weng의 포스트 내용을 원저자 동의하에 번역한 내용입니다.)
Policy Gradient Algorithms
Abstract: In this post, we are going to look deep into policy gradient, why it works, and many new policy gradient algorithms proposed in recent years: vanilla policy gradient, actor-critic, off-policy actor-critic, A3C, A2C, DPG, DDPG, D4PG, MADDPG, TRPO,
lilianweng.github.io
Policy Gradient
강화학습의 목적은 optimal reward를 얻기 위해서 agent에게 optimal한 behavior strategy를 찾는데 있다. 여러 알고리즘들이 있지만, policy gradient는 수식에서 보통 \(\pi\)라고 표현되는 policy를 직접적으로 모델링하고 최적화하는데 주력하며, 보통은 \(\theta\)라고 하는 특정 parameter로 구성된 함수, \(\pi_{\theta}\) 로 표현된다. Bellman equation에 나오는 reward (objective) function의 값은 이 policy의 영향을 받고, 해당 알고리즘을 적용한 방법들은 보통 최적의 reward를 얻는데있어 이 \(\theta\)를 최적화하는 경향을 띄고 있다.
reward function은 다음과 같이 정의된다.
$$ J(\theta) = \sum_{s \in S} d^{\pi}(s)V^{\pi}(s) = \sum_{s \in S}d^{\pi}(s) \sum_{a \in A} \pi_{\theta}(a|s)Q^{\pi}(s, a) $$
여기서 \(d^{\pi}(s)\)는 policy \(\pi_{\theta}\)를 가진 상태의 markov chain에 대한 stationary distribution이다. (다른게 표현하면 policy \(\pi_{\theta}\)에 대한 on-policy state distribution) 여기서 policy \(\pi_{\theta}\)의 \(\theta\)는 생략되어서 표현되곤 한다. 예를 들어서 위의 \(d^{\pi}, Q^{\pi}\)란 표기도 정식대로 표기하면 policy \(\pi_{\theta}\)를 가진 상태이므로 \(d^{\pi_{\theta}}, Q^{\pi_{\theta}}\)라고 표기되어야 한다. Stationary distribution이란 용어가 이해가 어려울텐데, 만약 특정 environment상의 markov chain을 가진 state를 계속 이동한다고 가정해보자. 그러면 시간이 끝까지 흘러가게 되면, 어느 특정 state에 도달하게 될 확률은 어느 한 값으로 수렴하게 될텐데, 이걸 policy \(\pi_{\theta}\)에 대한 stationary probability가 되는 것이다. 그러면 stationary distribution \(d^{\pi}(s) = \lim_{t \to \infty} P(s_{t} = s | s_{0}, \pi_{\theta} ) \)는 state \(s_{0}\)에서 시작해서 t step동안 policy \( \pi_{\theta} \)에 따라 action을 취할 때 \(s_{t} = s\)일 확률을 나타내게 된다. 사실 Markov chain에 대한 stationary distribution는 Google 검색 엔진에 들어가 있는 PageRank algorithm을 구성하는 주요 요건이기도 하다. 이에 대해서 확인해보려면, 이 글을 읽어보면 좋을거 같다.
Policy-based method가 continuous space를 가지는 environment 상에서 조금 더 유용한 것은 당연하다. 왜냐하면, value function의 value을 estimate하기에는 무한의 action과 state가 존재하고 value-based approach는 continuous space를 가진 environment에서 계산하기에는 너무 힘들기 때문이다. 예를 들어 generalized policy iteration 기법같은 경우에는 policy를 improve하는 step인 \( arg \max_{a \in A} Q^{\pi} (s, a) \)에서는 action space에 대한 전체 탐색이 필요한데, 이렇게 되면 curse of dimensionality가 발생하게 된다.
gradient ascent 기법을 사용하면, 가장 큰 return을 줄 수 있는 policy \( \pi_{\theta} \)에서 \(\theta\)를 찾는데 있어 policy gradient인 \( \nabla_{\theta} J(\theta) \)이 이끄는 방향대로 \(\theta\)를 바꿀 수 있게 된다.
Policy Gradient Theorem
policy gradient \( \nabla_{\theta} J(\theta)\)를 계산하는 것은 전체 동작에 있어서 매우 유용한 동작인데, 이 계산이 (\( \pi_{\theta}\) 에 의해 직접적으로 결정되는) action selection과 (\( \pi_{\theta}\) 에 의해 간접적으로 결정되는) target selecton behavior에 의한 stationary distribution에 영향을 주기 때문이다. 주어진 environment가 unknown이면, policy가 update되면서 state distribution \(d^{\pi}(s)\) 이 어떻게 바뀌게 될지 estimate하는 것이 어렵기 때문이다.
다행히도 policy gradient theorem이 이런 문제를 해결할 수 있다. 이를 활용하면, objective function에 대한 derivative를 앞에서 문제로 작용했던 \(d^{\pi}(.)\) 와 관련되지 않게끔, 식을 재구성해주고, gradient를 계산하는 \(\nabla_{\theta}J(\theta)\) 도 매우 간략하게 해준다.
$$ \begin{align} \nabla_{\theta} J(\theta) &= \nabla_{\theta} \sum_{s \in S} d^{\pi}(s) \sum_{a \in A} Q^{\pi} (s, a) \pi_{\theta} (a|s) \\ &\propto \sum_{s \in S}d^{\pi}(s) \sum_{a \in A} Q^{\pi}(s,a) \nabla_{\theta} \pi_{\theta} (a | s) \end{align} $$
(\( \because d^{\pi}(s), Q^{\pi}(s,a)\) 가 \(\theta\)에 관한 함수가 아니기 때문이다.)
Proof of Policy Gradient Theorem
이번 장은 Sutton 책 13.1절에 나와있는 증명을 따라가보고, 왜 policy gradient theorem이 맞는지에 대해서 규명해보고자 한다.
먼저 state-value function의 derivative에서 시작해본다.
$$ \begin{align} & \nabla_{\theta} V^{\pi}(s) \\
&= \nabla_{\theta} \Big( \sum_{a \in A} \pi_{\theta} (a|s) Q^{\pi}(s, a) \Big) \\
&= \sum_{a \in A} \Big( \nabla_{\theta} \pi_{\theta} (a|s) Q^{\pi}(s, a) + \pi_{\theta}(a|s) \color{red}{ \nabla_{\theta} Q^{\pi}(s, a)} \Big) & \scriptstyle{\text{; Derivative product rule.}} \\
&= \sum_{a \in A} \Big( \nabla_{\theta} \pi_{\theta} (a|s) Q^{\pi}(s, a) + \pi_{\theta}(a|s) \color{red}{\nabla_{\theta} \sum_{s', r} P(s', r| s, a)(r + V^{\pi} (s'))} \Big) & \scriptstyle{\text{; Extend } Q^\pi \text{ with future state value.}} \\ &= \sum_{a \in A} \Big( \nabla_{\theta} \pi_{\theta} (a|s) Q^{\pi}(s, a) + \pi_{\theta}(a|s) \color{red}{\sum_{s', r} P(s', r | s, a) \nabla_{\theta} V^{\pi}(s')} \Big) & \scriptstyle{P(s',r \vert s,a) \text{ or } r \text{ is not a func of }\theta} \\ &= \sum_{a \in A} \Big( \nabla_{\theta} \pi_{\theta}(a|s) Q^{\pi}(s, a) + \pi_{\theta}(a|s) \color{red}{ \sum_{s'} P(s' | s, a) \nabla_{\theta} V^{\pi} (s')} \Big) & \scriptstyle{\text{; Because } P(s' \vert s, a) = \sum_r P(s', r \vert s, a)} \end{align} $$
위의 식을 통해서 아래의 수식을 도출할 수 있다.
$$ \color{red}{ \nabla_{\theta} V^{\pi}(s)} = \sum_{a \in A} \Big( \nabla_{\theta} \pi_{\theta} (a|s) Q^{\pi}(s, a) + \pi_{\theta}(a|s) \sum_{s'} P(s' | s, a) \color{red}{\nabla_{\theta} V^{\pi}(s')} \Big) $$
잘 보면 알겠지만 빨간 term이 recursive하게 반복되는 것을 볼 수 있고, future state-value function \( V^{\pi}(s')\) 이 같은 방정식을 통해서 계속 반복적으로 풀어지는 것도 확인할 수 있다.
그러면 이제 policy \(\pi_{\theta}\)에 따라 state \(s\)에서 시작해서, k step 후에 state \(x\)에 도달하는 transition의 probability를 \(\rho^{\pi}(s \to x, k) \) 라고 하고, 이에 따른 전개를 살펴보자.
$$ s \xrightarrow[]{a \sim \pi_\theta(.\vert s)} s' \xrightarrow[]{a \sim \pi_\theta(.\vert s')} s'' \xrightarrow[]{a \sim \pi_\theta(.\vert s'')} \dots $$
- k = 0 : \( \rho^{\pi}(s \to s, k = 0) = 1 \)
- k = 1 : 해당 state에서 취할 수 있는 모든 행동을 수행한 후에, target state까지 걸리는 transition probability를 모두 더한 형태가 된다 : \(\rho^{\pi}(s \to s', k = 1) = \sum_{a} \pi_{\theta}(a|s)P(s'|s, a) \)
- 이제 목표를 policy \(\pi_{\theta}\)에 따라 움직일때 state \(s\)에서 시작해서 k+1 step후에 state \(x\)에 도달하는 걸로 가정해보자. 먼저 위에 도식화한 것과 같이 k step까지는 state \(s\)에서 state \(s'\)으로 이동할 수 있다. (state \(s'\)는 아무 곳이나 될 수 있다. \( s' \in S\))
그리고 마지막 step에 state \(x\)에 도달하는 형태가 될 것이다. 이렇게 될 경우, transition probability를 recursive하게 update할 수 있게 된다. : \(\rho^{\pi}(s \to x, k+1) = \sum_{s'} \rho^{\pi}(s \to s', k)\rho^{\pi}(s' \to x, 1) \)
이제 앞에서 다뤘던 recursive형태의 \( \nabla_{\theta} V^{\pi}(s) \)를 푸는 작업을 다시 해보자. 일단 식을 좀 간단히 해보기 위해 \( \phi(s) = \sum_{a \in A} \nabla_{\theta} \pi_{\theta} (a|s) Q^{\pi}(s, a) \)라고 축약하겠다. \( \nabla_{\theta} V^{\pi}(.) \)를 무한대로 계속 확장시키다보면, state \(s\)에서 시작해서 특정 step 후에 어느 state로든 transition이 가능하고, 이때의 visitation probability를 모두 더함으로써 \( \nabla_{\theta} V^{\pi}(s) \)를 쉽게 구할 수 있을 것이다.
$$ \begin{align} & \color{red}{\nabla_{\theta} V^{\pi}(s)} \\
&= \phi(s) + \sum_{a} \pi_{\theta}(a|s) \sum_{s'}P(s'|s, a) \color{red}{\nabla_{\theta}V^{\pi}(s')} \\
&= \phi(s) + \sum_{s'} \sum_{a} \pi_{\theta}(a|s) P(s'|s, a) \color{red}{\nabla_{\theta} V^{\pi}(s')} \\
&= \phi(s) + \sum_{s'} \rho^{\pi}(s \to s', 1) \color{red}{\nabla_{\theta}V^{\pi}(s')} \\
&= \phi(s) + \sum_{s'} \rho^{\pi}(s \to s', 1) \color{red}{[\phi(s') + \sum_{s''} \rho^{\pi}(s' \to s'', 1) \nabla_{\theta} V^{\pi}(s'') ]} \\
&= \phi(s) + \sum_{s'} \rho^{\pi}(s \to s', 1) \phi(s') + \sum_{s''} \rho^{\pi} (s \to s'', 2) \color{red}{\nabla_{\theta} V^{\pi}(s'')} \scriptstyle{\text{ ; Consider }s'\text{ as the middle point for }s \to s''}\\
&= \phi(s) + \sum_{s'} \rho^{\pi} (s \to s', 1) \phi(s') + \sum_{s''} \rho^{\pi} (s \to s'', 2) \phi(s'') + \sum_{s'''} \rho^{\pi} (s \to s''', 3) \color{red}{\nabla_{\theta} V^{\pi}(s''')} \\
&= \dots \scriptstyle{\text{; Repeatedly unrolling the part of }\nabla_\theta V^\pi(.)} \\
&= \sum_{x \in S} \sum_{k=0}^{\infty} \rho^{\pi} (s \to x, k) \phi(x)
\end{align}$$
이를 이용해서 Q-value function에 대한 derivative \( \nabla_{\theta} Q^{\pi}(s, a) \) 를 없앨 수 있게 된다. 이 값을 objective function \( J(\theta)\)에 넣게 되면, 다음과 같은 과정을 수행할 수 있다.
$$ \begin{align} \nabla_{\theta} J(\theta) &= \nabla_{\theta} V^{\pi} (s_{0}) & \scriptstyle{\text{; Starting from a random state } s_0} \\
&= \sum_{s} \color{blue}{\sum_{k=0}^{\infty} \rho^{\pi} (s_{0} \to s, k)} \phi(s) &\scriptstyle{\text{; Let }\color{blue}{\eta(s) = \sum_{k=0}^\infty \rho^\pi(s_0 \to s, k)}} \\
&= \sum_{s} \eta(s)\phi(s) \\
&= \Big( \sum_{s} \eta(s) \Big) \sum_{s} \frac{\eta(s)}{\sum_{s}\eta(s)} \phi(s) & \scriptstyle{\text{; Normalize } \eta(s), s\in\mathcal{S} \text{ to be a probability distribution.}} \\
&\propto \sum_{s} \frac{\eta(s)}{\sum_{s} \eta(s)} \phi(s) &\scriptstyle{ \sum_{s} \eta(s) \text{ is a constant}} \\ &= \sum_{s} d^{\pi}(s) \sum_{a} \nabla_{\theta} \pi_{\theta} (a|s) Q^{\pi}(s, a) &\scriptstyle{d^{\pi}(s) = \frac{\eta(s)}{\sum_{s} \eta(s)} \text{ is stationary distribution.}}
\end{align} $$
episode로 동작하는 경우(episodic case), propotionality 상수 (\(\sum_{s} \eta(s)\))는 episode의 average length가 되고, 연속해서 동작하는 경우(continuing case, 즉 termination이 없는 경우), 해당 값은 1이 된다. (Sutton and Barto 책 13.2절 참고) 그러면 gradient는 다음과 같이 다시 정리할 수 있게 된다.
$$ \begin{align} \nabla_{\theta} J(\theta) &\propto \sum_{s \in S} d^{\pi} (s) \sum_{a \in A} Q^{\pi}(s, a) \nabla_{\theta} \pi_{\theta} (a|s) \\ &= \sum_{s \in S} d^{\pi}(s) \sum_{a \in A} \pi_{\theta} (a|s) Q^{\pi}(s, a) \frac{ \nabla_{\theta} \pi_{\theta} (a|s)}{\pi_{\theta}(a|s)} \\
&= \mathbb{E}_{\pi} [ Q^{\pi}(s, a) \nabla_{\theta} \ln \pi_{\theta} (a|s)] &\scriptstyle{\text{; Because } (\ln x)' = \frac{1}{x}} \end{align} $$
여기서 \( \mathbb{E}_{\pi} \) 는 policy \( \pi_{\theta} \)를 따를 때, state distribution과 action distribution 상태에서의 평균값, \( \mathbb{E}_{s \sim d_{\pi}, a \sim \pi_{\theta}} \)를 말하고, 결국 이 뜻은 on policy 상태에서의 평균값을 구하는 것과 동일하게 된다.
policy gradient theorem은 수많은 policy gradient algorithm의 이론적인 기반을 제공해준다. 가장 기초적인 vanila policy gradient update는 bias는 없지만 variance가 높다. 후속으로 나온 algorithm들은 bias를 변화시키지 않은 상태에서 variance를 줄이는데 초점을 맞췄다.
$$ \nabla_{\theta} J(\theta) = \mathbb{E}_{\pi} [ Q^{\pi}(s, a) \nabla_{\theta} \ln \pi_{\theta} (a|s) ] $$
GAE (General advantage estimation) 기법을 적용한 policy gradient method를 설명한 paper(schulmann et al, 2016)에 대한 간략한 요약과 GAE를 구성하는 몇몇 요소들에 대해 심도있게 다룬 포스트들이 있는데, 한번 읽어볼 것을 권한다.

Policy Gradient Algorithms
몇년동안 수많은 policy gradient algorithm들이 나와, 다 다룰 여건이 되지는 않지만, 읽어봐야 할 몇몇 algorithm에 대해서 소개를 해보고자 한다.
REINFORCE
REINFORCE (Monte-Carlo policy gradient)는 episode 샘플 내에서 Monte-Carlo method를 통해 구한 estimated return을 가지고 policy parameter \( \theta \)를 update해 나가는 기법이다. REINFORCE는 sample내에서의 gradient에 대한 expectation이 actual 내에서의 gradient에 대한 expectation이 같기 때문에 효과가 있다. 아래의 식을 보면 알 수 있다.
$$ \begin{align} \nabla_{\theta} J(\theta) &= \mathbb{E}_{\pi} [Q^{\pi}(s,a) \nabla_{\theta} \ln \pi_{\theta} (a|s)] \\ &= \mathbb{E}_{\pi} [G_{t} \nabla_{\theta} \ln \pi_{\theta} (A_{t} | S_{t})] &\scriptstyle{\text{; Because } Q^{\pi}(S_{t}, A_{t}) = \mathbb{E}_{\pi}[G_{t}|S_{t}, A_{t}]} \end{align} $$
이를 통해서 real sample trajectory들로부터 total expected return \( G_{t}\)를 구할 수 있게 되었고, 이를 이용해서 policy gradient를 update할 수 있게 되었다. 이때 전체 trajectory를 활용하게 되고, 이때문에 Monte-Carlo method라고 부르는 것이다.
절차는 매우 직관적이다.
- 처음에 policy parameter \( \theta \)를 랜덤하게 지정한다.
- 해당 policy parameter \( \theta\)를 가진 policy \(\pi_{\theta} \)를 통해서 trajectory를 생성한다.
: \(S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, ... , S_{T} \) - \(t = 1, 2, .. T \) 에 대해서
- total expected return \(G_{t}\)를 estimate한다.
- 이를 바탕으로 policy parameter를 업데이트한다.
: \( \theta \leftarrow \theta + \alpha \gamma^{t} G_{t} \nabla_{\theta} \ln \pi_{\theta} (A_{t} | S_{t}) \)
REINFORCE가 가장 많이 쓰이는 형태는 bias를 변하지 않게 하는 상태로 gradient estimation에 대한 variance를 줄이기 위해서 total expected return \(G_{t}\)에서 baseline value를 빼는 것이다. (가능하면 bias를 유지한 상태에서 variance를 낮추고 싶은 것이다.) 예를 들어, 가장 많이 쓰이는 baseline이 state-action value (\(Q(s, a)\)에서 state value를 빼는 것인데, 위의 방법을 적용하고 싶으면, gradient ascent update시 advantage function (\(A(s, a) = Q(s, a) - V(s)\))를 사용하면 되는 것이다. 다른 포스트에서 왜 이런 baseline이 variance를 줄이는데 도움이 되는지를 policy gradient에 대한 기본적인 내용에 덧붙여서 잘 설명하고 있다.
Actor-Critic
policy gradient에서 두개의 핵심 요소는 policy model과 value function이다. policy를 학습하는데 덧붙여서 value function을 학습하는 것도 좋은 성능을 보여주는데, value function을 이해하는 것 자체가 vanila policy gradient에서 gradient varience를 줄이는 것처럼 policy를 update하는데 도움을 주기 때문이다. 이게 바로 Actor-Critic method가 추구하는 것이다.
Actor-critic method는 두 개의 모델로 구성되어 있는데, 어떨 때는 서로의 모델이 parameter를 공유하는 경우도 있다:
- Critic 모델은 algorithm내 사용되는 value function (state-action value function \(Q_{w}(a|s)\)이거나 state value function \(V_{w}(s)\)를 결정할 value function parameter \(w\)를 update한다.
- Actor 모델은 critic 모델이 제안한 방향대로, 현재의 policy \( \pi_{\theta}(a|s)\)를 결정할 parameter \(\theta\)를 update한다.
그러면 이제 간단한 action-value actor-critic algorithm이 어떻게 동작하는지를 살펴보겠다.
- 초기에 \(s, \theta, w\)를 랜덤하게 초기화하고, policy \(\pi_{\theta}(a|s)\)에 기반해 action \(a\)를 샘플링한다. (\(a \sim \pi_{\theta}(a|s)\))
- \(t = 1, 2, .. T \) 에 대해서
- reward \(r_{t} \sim R(s, a)\)와 next state \(s' \sim P(s'|s, a)\)를 sampling한다.
- next state \(s'\)를 이용해서 policy \( \pi_{\theta}(a' | s')\)로부터 next action \(a'\)를 sampling한다. (\(a' \sim \pi_{\theta}(a'|s')\))
- policy parameter \(\theta\)를 update한다: \(\theta \leftarrow \theta + \alpha_{\theta} Q_{w}(s, a) \nabla_{\theta} \ln \pi_{\theta}(a|s) \)
- 앞에서 구한 reward를 가지고, time t에서의 state-action value에 대한 correction(TD error)을 계산한다.
: \(\delta_{t} = r_{t} + \gamma Q_{w}(s', a') - Q_{w}(s, a) \)
그리고 이 값을 활용해서 state-action value function의 parameter \(w\)를 update한다.
: \(w \leftarrow w + \alpha_{w} \delta_{t} \nabla_{w} Q_{w}(s, a) \) - action과 state를 update한다.
: \( a \leftarrow a', s \leftarrow s' \)
여기서 두 개의 learning rate parameter \( \alpha_{\theta}, \alpha_{w} \)가 나오는데, 각각 policy parameter와 value function parameter를 update하기 위해 미리 정의된 hyperparameter이다.
Off-Policy Policy Gradient
앞에서 소개한 REINFORCE나 vanila actor-critic method는 on-policy policy gradient method이다. 즉, 우리가 최적화해서 구하기를 원하는 target policy와 매우 유사한 policy로부터 training sample이 수집되어야 한다는 것이다. Off-policy method는 on-policy와 반대로 몇가지 이점을 가져올 수 있다.
- Off-policy 방법은 full trajectory가 필요하지 않기 때문에, sample efficiency 측면에서 지난 episode에서 trajectory를 뽑아서 재사용할 수 있다. (이때 사용하는 것이 "experience replay"이다.)
- Sample trajectory가 우리가 구하고자 하는 target policy와는 다른 behavior policy로부터 구할 수 있는데, 이를 통해서 exploration 측면에서 더 좋을 수 있다.
이제 off-policy policy gradient가 어떻게 계산되는지를 살펴보고자 한다. sample을 수집하는데 사용된 behavior policy는 (마치 hyperparameter를 미리 지정하는 것과 같은) known policy인데, 이를 \(\beta(a|s)\)라고 해보겠다. 그러면 objective function은 behavior policy 에 의해서 정의된 state distribution에서 계산한 reward를 모두 더한 값이 되겠다.
$$ J(\theta) = \sum_{s \in S} d^{\beta}(s) \sum_{a \in A} Q^{\pi} (s, a) \pi_{\theta} (a|s) = \mathbb{E}_{s \sim d^{\beta}}[\sum_{a \in A} Q^{\pi}(s, a) \pi_{\theta}(a|s)] $$
위 식에서 \(d^{\beta}(s)\)는 behavior policy \(\beta\)에 따른 stationary distribution이 된다. 여기서 \(d^{\beta}(s) = \lim_{t \to \infty} P(S_{t} = s | S_{0}, \beta)\) 이고, \(Q^{\pi}\)는 (Behavior policy \(\beta\)가 아닌) target policy \(\pi\) 에 대해서 estimated된 state-action value function 이라는 것을 기억하자.
Behavior Policy \(\beta(a|s)\)에 의해 나온 action \(a\)를 통해 training observation을 sampling했을 때, 이에 대한 gradient를 다음과 같이 다시 써볼 수 있다.
$$ \begin{align} \nabla_{\theta} J(\theta) &= \nabla_{\theta} \mathbb{E}_{s \sim d^{\beta}} \Big[ \sum_{a \in A} Q^{\pi}(s, a) \pi_{\theta}(a|s) \Big] \\ &= \mathbb{E}_{s \sim d^{\beta}} \Big[ \sum_{a \in A} \big( Q^{\pi} (s, a) \nabla_{\theta} \pi_{\theta} (a|s) + \color{red}{\pi_{\theta}(a|s) \nabla_{\theta} Q^{\pi}(s, a)} \big) \Big] &\scriptstyle{ \text{; Derivative product rule. }} \\ &\stackrel{(i)}{\approx} \mathbb{E}_{s \sim d^{\beta}} \Big[ \sum_{a \in A} Q^{\pi}(s, a) \nabla_{\theta} \pi_{\theta}(a|s) \Big] &\scriptstyle{\text{; Ignore the red part: } \color{red}{\pi_{\theta}(a|s) \nabla_{\theta} Q^{\pi}(s, a)} } \\ &= \mathbb{E}_{s \sim d^{\beta}} \Big[ \sum_{a \in A} \beta(a|s) \frac{\pi_{\theta}(a|s)}{\beta(a|s)} Q^{\pi}(s, a) \frac{\nabla_{\theta} \pi_{\theta}(a|s)}{\pi_{\theta}(a|s)} \Big] \\ &= \mathbb{E}_{\beta} \Big[ \color{blue}{ \frac{\pi_{\theta}(a|s)}{\beta(a|s)}} Q^{\pi}(s, a) \nabla_{\theta} \ln \pi_{\theta} (a|s) \Big] &\scriptstyle{\text{; The blue part is the importance weight}} \end{align} $$
여기서 \( \frac{\pi_{\theta}(a|s)}{\beta(a|s)} \)를 importance weight라고 부른다. \(Q^{\pi}\)가 target policy에 대한 state-action value function이기 때문이기도 하고, 또한 policy parameter \(\theta\)에 대한 함수이기도 하기 때문에 product rule을 적절히 사용해서 \( \nabla_{\theta} Q^{\pi}(s, a)\) 에 대한 derivative를 구해야 한다. 하지만 target policy를 모르는 현실 상에서 \( \nabla_{\theta} Q^{\pi}(s, a) \)를 계산하는 것은 거의 불가능하다. 다행히도 앞의 수식 전개에서 무시했던 Q에 대한 gradient를 이용해서 approximated gradient를 사용한다면, 적어도 policy improvement가 이뤄지고, 궁극적으로 true local minimum에 도달할 수 있는 것을 보장할 수 있다. 여기(Degris, White & Sutton, 2012) 에 증명식이 나와 있다.
요약하자면, off-policy 에 맞춰 policy gradient를 적용할 경우, 이를 weighted sum을 통해서 조정할 수 있고, 이 때의 weight는 behaivor policy와 target policy간의 비율인 importance weight \(\frac{\pi_{\theta}(a|s)}{\beta(a|s)}\) 가 된다.
A3C (Asynchronous Advantage Actor-Critic)
Asynchronous Advantage Actor-Critic (Mnih et al., 2016), 짧게 A3C라고 불리는 이 algorithm은 parallel training에 초점을 맞춘 classic policy gradient method이다.
A3C에서, Critic 모델은 여러 개의 Actor 모델이 병렬적으로 학습되면서 global parameter를 통해 시간 단위로 동기화되는 동안, value function을 학습한다. 결국, A3C는 parallel training 환경에서 잘 동작하도록 설계되었다.
우선 state value function을 예로 한번 들어보겠다. state value function에 대한 loss function은 \( J_{v}(w) = (G_{t} - V_{w}(s))^2 \)에 대한 mean squared error를 최소화 하려는 목적이 있고, 이때 gradient descent를 통해 optimal \(w\)를 찾을 수 있다. 이 때의 state value function은 policy gradient update시 baseline으로 활용할 수 있다.
algorithm은 다음과 같이 동작한다.
- Synchronization을 위한 global parameter \(\theta, w\)와 thread용 parameter \(\theta' , w'\)를 선언하고 초기화한다.
- \(t = 1 \)로 time step을 초기화 한다.
- \(T \le T_{MAX} \)인 동안
- gradient를 초기화한다
: \(d\theta = 0, dw = 0\) - thread 전용 parameter를 global parameter와 synchronize시킨다.
: \( \theta' = \theta , w' = w \) - \(t_{start} = t\)로 설정하고 starting state \(s_{t}\)를 sampling한다.
- (\(s_{t} != TERMINAL\))이고, \(t - t_{start} \le t_{max} \)인 동안:
- policy \(\pi_{\theta'} (a_{t} | s_{t})\)로부터 action \(a_{t}\)를 수행하고,\(a_{t} \sim \pi_{\theta'}(a_{t}|s_{t})\)), 이에 대한 새로운 reward \(R_{t}\)와 새로운 state \(s_{t+1}\)를 얻어온다.
- time을 update한다.
: \(t = t+1, T = T+1\)
- estimated return을 담을 변수를 초기화하고, 조건에 맞게 정의한다.
\( R = \begin{cases} 0 & \text{if} s_{t} \text{ is TERMINAL} \\ V_{w'}(s_{t}) & \text{otherwise} \end{cases} \) - \(i = t-1, ... t_{start} \) 까지
- \(R \leftarrow r_{i} + \gamma R\)
- thread 전용 parameter \(\theta'\)에 대해서 gradient를 accumulate한다.
: \( d\theta \leftarrow d\theta + \nabla_{\theta'} \log \pi_{\theta'} (a_{i} | s_{i}) (R - V_{w'}(s_{i})) \)
thread 전용 parameter \(w'\)에 대해서 gradient를 accumulate한다.
: \( dw \leftarrow dw + 2(R - V_{w'}(s_{i})) \nabla_{w'}(R - V_{w'}(s_{i})) \)
- \( \theta, w \) 를 \( d\theta, dw \)를 이용해서 asynchronous하게 update해준다
- gradient를 초기화한다
A3C 자체가 여러 agent를 학습시키는데 있어 parallelism이 가능하게끔 해줬는데, 그 중에서도 특히 위의 algorithm 전개 중 6.2 부분이 loss를 줄이는데 사용되는 minibatch-based stochastic gradient descent를 parallel하게 동작하도록 수정된 부분이다. 해당 부분이 바로 학습 thread가 각기 얻은 결과를 통해 \(w, \theta\)를 수정해가는 것이다.
A2C (Advantage Actor Critic)
A2C 는 앞에서 소개한 A3C의 Synchoronous, Deterministic version이다. 그래서 A3C 중 앞의 "A" (Asynchronous)가 진 이유이기도 하다. A3C에서 각 agent는 각각 독립적으로 global parameter에 자신의 state에 대해 전달했었기 때문에, 때때로는 thread별로 동작하는 agent에 다른 version의 policy가 수행되면서, update된 policy의 결과가 optimal하지 않을 가능성이 존재했었다. 이런 문제를 해결하기 위해서 A2C에서는 coordinator가 있어서 global parameter를 update하기전에 각 agent에서 동작하는 학습이 끝날때까지 기다리고, 다음 iteration에 모든 agent가 같은 policy를 가지고 병렬적으로 수행할 수 있도록 해준다. 이렇게 동기화된 gradient update는 학습을 조금더 확실하게 해주고, 잠재적으로는 convergence를 빠르게 할 수 있도록 해준다.
OpenAI의 글에서 언급되다시피 A2C는 A3C에 비해서 GPU를 효율적으로 사용하고, 큰 batch size를 가지고 학습하는 경우에도 A3C와 같거나 더 나은 성능을 보여준다.

DPG (Deterministic Policy Gradient)
[논문 | 코드]
위에서 소개한 방법에서, policy function \( \pi(\cdot|s)\) 는 주어진 state \(s\)상에서 action \(A\)에 대한 probability distribution을 모델링한 것이기 때문에, stochastic하다. 반대로 Deterministic Policy Gradient (DPG)는 policy를 deterministic decision을 하는 것(\(a = \mu(s)\))으로 모델링한다. policy가 single action을 내뱉을때, 이에 대한 policy function의 gradient를 계산한다는 것 자체가 이상하게 들릴 수 있다. 한번 하나하나씩 살펴보고자 한다.
글의 전개를 위해서 앞에서 다뤘던 몇가지 표현을 다시 언급해본다.
- \( \rho_{0}(s) \) : state에 대한 initial distribution
- \( \rho^{\mu} (s \to s', k) \) : state \(s\)에서 시작했을때, policy \(\pi\)에 따라서 k step 후 state \(s'\)에 도달하기까지의 visitation probability density
- \( \rho^{\mu}(s') \) : Discounted state distribution. 다음과 같이 정의된다.
\( \rho^{\mu}(s') = \int_{s} \sum_{k=1}^{\infty} \gamma^{k-1} \rho_{0} (s) \rho^{\mu}(s \to s', k) ds \)
여기서 우리가 최적화해야 할 objective function은 다음과 같다.
$$ J(\theta) = \int_{s} \rho^{\mu}(s) Q(s, \mu_{\theta}(s)) ds $$
Deterministic Policy Gradient Theorem : 이제 gradient를 계산해볼 차례이다. chain rule에 따르면, 우선 action \(a\)에 대해 Q의 gradient를 구하고, policy parameter \(\theta\)에 대해 deterministic policy function \( \mu\)의 gradient를 구할 것이다.
$$ \begin{align} \nabla_{\theta} J(\theta) &= \int_{s} \rho^{\mu}(s) \nabla_{a} Q^{\mu}(s, a) \nabla_{\theta} \mu_{\theta}(s)|_{a=\mu_{\theta}(s)} \\ &= E_{s \sim \rho^{\mu}} [ \nabla_{a} Q^{\mu}(s, a) \nabla_{\theta} \mu_{\theta}(s)|_{a=\mu_{\theta}(s)}] \end{align} ds$$
여기서 deterministic policy를 stochastic policy의 특별한 경우라고 생각해볼 수 있는데, 가령 한 action에 대한 probability distribution이 0이 아닌 유일한 값만 가지는 경우가 그렇다. 사실 DPG 논문에서, 저자는 만약 현재의 stochastic policy \( \pi_{\mu_{\theta}, \sigma} \)가 deterministic policy \( \mu_{\theta}\)와 variation variable \( \sigma \)에 의해서 re-parameterized 되는 경우, stochastic policy는 \( \sigma = 0 \) 일때 결과적으로 deterministic policy와 동일하다는 것을 보여줬다. deterministic policy와 비교했을 때, stochastic policy가 전체 state와 action space에 대해서 데이터를 완성해야 한다는 측면에서 더 많은 샘플이 필요할 거라 기대한다.
Deterministic policy gradient theorem은 일반적인 policy gradient framework에 적용해볼 수 있다.
이제 과정을 증명하기 위해서 on-policy actor-critic algorithm의 예를 살펴보자, on-policy actor-critic 이 매번 수행될때마다, \( a = \mu_{\theta}(s) \)에 의해서 두개의 action이 deterministic하게 선택되며, SARSA algorithm은 아래에서 계산될 새로운 gradient에 따라서 on-policy parameter를 update한다.
$$ \begin{align} \delta_{t} &= R_{t} + \gamma Q_{w}(s_{t+1}, a_{t+1}) - Q_{w}(s_{t}, a_{t}) & \scriptstyle{\text{TD error in SARSA}} \\ w_{t+1} &= w_{t} + \alpha_{w} \delta_{t} \nabla_{w} Q_{w} (s_{t}, a_{t}) \\ \theta_{t+1} &= \theta_{t} + \alpha_{\theta} \color{red}{ \nabla_{a} Q_{w} (s_{t}, a_{t}) \nabla_{\theta} \mu_{\theta}(s)|_{a=\mu_{\theta}(s)}} & \scriptstyle{\text{ Deterministic policy gradient theorem }} \end{align} $$
하지만 environment내에 sufficient noise가 있지 않는한, policy의 determinacy로 인해서, 충분한 exploration이 이뤄지는 것을 보장하기가 매우 어렵다. 그래서 policy에 noise를 더하거나,(역설적이게도 이렇게 noise를 더하면 policy가 nondeterministic하게 된다..) 아니면 샘플을 모아서 다른 stochastic behaior policy를 수행하게 함으로써 off-policy처럼 학습하게 하는 방법을 취할 수 있다.
off-policy approach라는 건 training trajectory가 stochastic policy \( \beta(a|s) \)에 의해서 생성되고, 이로 인해 state distribution이 discounted state density \( \rho^{\beta} \) 를 따르게 되는 것이다.
$$ \begin{align} J_{\beta}(\theta) &= \int_{s} \rho^{\beta} Q^{\mu} (s, \mu_{\theta}(s))ds \\
\nabla_{\theta}J_{\beta}(\theta) &= E_{s \sim \rho^{\beta}} [ \nabla_{a} Q^{\mu} (s, a) \nabla_{\theta} \mu_{\theta}(s)|_{a = \mu_{\theta}(s)}] \end{align} $$
여기서 policy가 deterministic하기 때문에, 주어진 state \(s\)에 대한 estimated reward를 구할 때, \( \sum_{a} \pi(a|s) Q^{\pi}(s,a) \)를 구할 필요 없이, \( Q^{\mu}(s, \mu_{\theta}(s)) \) 만 알면 된다. 이렇게 stochastic policy에 대해서 off-policy 기법을 적용할 때, behavior와 target policy간의 오차를 보정해주기 위해서 importance sampling을 사용하곤 하는데, 이 부분에 대해서는 위(off-policy policy gradient)에서 설명했다. 하지만 deterministic policy gradient가 action에 대한 integral을 제거해주기 때문에, importance sampling 사용을 피할 수 있다.
DDPG (Deep Deterministic Policy Gradient)
Deep Deterministic Policy Gradient를 줄인, DDPG(Lillicrap et al, 2015)는 DPG에 DQN을 결합시킨 model-free off-policy actor-critic algorithm이다. DQN (Deep Q-Network)에 대해서 다시 다뤄보자면, experience replay과 frozen target network를 통해서 Q-function에 대한 학습을 안정화시킨 효과를 나타낸다. 원래의 DQN은 discrete space상에서 동작하지만, DDPG는 actor-critic framework를 활용하여 deterministic policy를 학습하면서, 효과를 continuous space까지로 확장시켰다.
좀 더 나은 exploration을 하기 위해서, exploration policy \( \mu' \)는 noise \(N\)을 추가함으로써 만들 수 있다.
$$ \mu'(s) = \mu_{\theta}(s) + N $$
추가로 DDPG는 ("conservation policy iteration"이라 부르는) soft update를 actor network 과 critic network의 parameter에 각각 적용한다. ( \(\tau \ll 1 \), \( \theta' \to \tau\theta + (1-\tau) \theta' \) ) 이 방법을 사용하면, target network이 천천히 변화가 강제로 발생하는데, 이 부분은 DQN에서 target network를 특정 period 동안 frozen 시키는 것과 다른 부분이다.
논문에서 유념히 볼 부분 중 하나는 robotics에서 활용되는 부분인데, low dimensional features에 대한 서로 다른 physical unit을 normalize 시키는 부분이다. 예를 들어 특정 모델이 policy를 학습하는데 있어 robot의 position과 velocity를 입력으로 받게끔 설계되어 있다. 이런 물리적 특정은 자연적으로 각기 다를 것이고, 같은 type 자체도 수많은 로봇내에서 그 특성이 다르기 때문에 학습이 어려울 것이다. 이때 Batch normalization을 사용해서, 샘플들을 하나의 minibatch에 넣고 모든 dimension에 대해서 normalize 시킴으로써 해결할 수 있다.

D4PG (Distributed Distributional DDPG)
Distributed Distributional DDPG (D4PG) 는 DDPG에 distributional 개념이 반영되도록 몇가지 개선점이 적용되었다.
(1) Distributional Critic : Critic network는 expected Q value를 하나의 random variable 로 estimate하는데, 이 random variable은 \(w \)에 의해서 parameterize되는 distribution \(Z_{w}\)를 가진다. 이를 통해서 Q value \(Q_{w}(s, a) = \mathbb{E}[Z_{w}(x, a)] \) 를 가지게 된다. 이 때 distributional parameter를 학습하는데 있어 초점을 맞출 loss는 두 개의 distributions 사이의 거리를 수치화시킨 어떤 값을 최소화하는 것이 될텐데, 논문에서는 이를 distributional TD error라고 표현하고 있다.
$$ L(w) = \mathbb{E}[d(\mathcal{T}_{\mu_{\theta}}, Z_{w'}(s, a), Z_{w}(s, a) ] $$
(위 식에서 \( d() \) 함수는 distance를 구하는 함수이고 \( \mathcal{T}_{\mu_{\theta}} \)는 Bellman operator이다.)
이를 이용해서 DPG에서 도출된 policy gradient update는 다음과 같이 바꿀 수 있다.
$$ \begin{align} \nabla_{\theta} J(\theta) & \approx \mathbb{E}_{\rho^{\mu}}[\nabla_{a} Q_{w}(s, a) \nabla_{\theta} \mu_{\theta}(s) |_{a=\mu_{\theta}(s)}] & \scriptstyle{ \text{; gradient update in DPG}} \\
&= \mathbb{E}_{\rho^{\mu}}[\color{red}{\mathbb{E}[\nabla_{a}Z_{w}(s, a)]} \nabla_{\theta} \mu_{\theta}(s) |_{a = \mu_{\theta}(s)}] & \scriptstyle{\text{; expectation of the Q-value distribution}} \end{align} $$
(2) \(N\)-step returns : TD-error를 계산할 때, future step에 얻어질 reward를 반영하기 위해서 one-step이 아닌, \(N\)-step TD target error를 구한다. 그래서 이에 따른 새로운 TD-target은 다음과 같이 정의된다:
$$ r(s_{0}, a_{0}) + \mathbb{E}[ \sum_{n=1}^{N-1} r(s_{n}, a_{n}) + \gamma^{N} Q(s_{N}, \mu_{\theta}(s_{N}))| s_{0}, a_{0} ]$$
(3) Multiple Distributed Parallel Actors : D4PG 는 \(K\)개의 Actor를 운용하면서, Parallel하게 experience를 수집하고, 같은 replay buffer에다가 data를 집어넣는다.
(4) Prioritized Experienced Replay (PER) : 마지막 수정된 부분은 size \(R\)의 replay buffer에서 non-uniform probability \(p_{i}\) 만큼 sampling을 수행하는 것이다. 이 방법을 통해서 sample \(i\)는 \( (Rp_{i})^{-1}\) 의 확률로 선택되게 되고, 이로 인해 importance weight는 \( (Rp_{i})^{-1} \)을 가지게 된다.

MADDPG (Multi-Agent Deep Deterministic Policy Gradient)
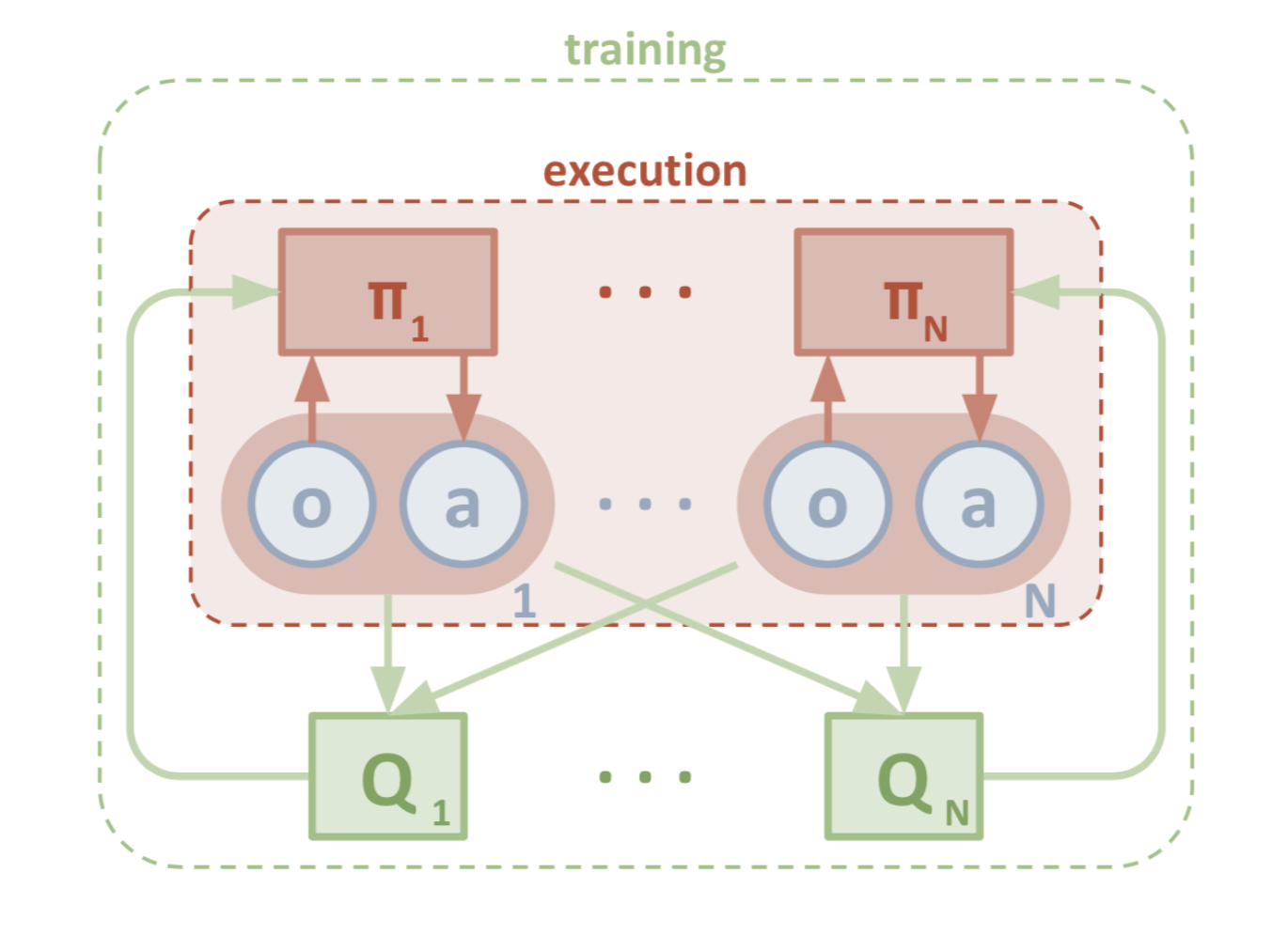
Multi-Agent DDPG (MADDPG) (Lowe et al, 2017)는 여러 개의 agent가 local information만 가지고, task를 처리할 수 있도록 서로 협력하는 환경으로 DDPG를 확장시킨 algorithm이다. agent 한개의 관점에서 볼때, environment는 non-stationary하고, 이때 다른 agent의 policy들은 빠르게 update되는데, 그 agent 입장에서는 unknown 상태로 남아있는 것이다. MADDPG는 이렇게 environment가 변하고, agent들간의 interaction을 처리할 수 있도록 actor-critic 모델이 재설계된 형태를 나타낸다.
여기서 RL 문제는 Markov games라고 알려져 있는, MDP의 Multi-agent 형태로 정형화시킬 수 있다. 다시 말해서, 총 \(N\)개의 agent가 있고, State의 집합 \(S\)가 있다고 가정해보자. 각 agent는 수행 가능한 action set \( A_{1}, ... , A_{N} \)이 있고, 관찰 가능한 observation set \( O_{1}, ... , O_{N} \)이 있다. 이때의 state-transtion function은 앞에서 언급한 모든 State, action, observation space와 연관되어 있다. \( \mathcal{T}: \mathcal{S} \times \mathcal{A}_1 \times \dots \mathcal{A}_N \mapsto \mathcal{S} \) 각 agent의 stochastic policy는 각 agent가 가진 state, action하고만 연관되어 있다: \(\pi_{\theta_i}: \mathcal{O}_i \times \mathcal{A}_i \mapsto [0, 1] \), 그리고 보통 deterministic policy라고 하는, 주어진 observation에 대한 action의 probability distribution은 다음과 같이 표현할 수 있다: \(\mu_{\theta_i}: \mathcal{O}_i \mapsto \mathcal{A}_i \)
여기서 observation과 deterministic policy를 하나의 vector 형태로 보고( \( \vec{o} = {o_1, \dots, o_N} , \vec{\mu} = {\mu_1, \dots, \mu_N} \) ), policy 역시 vector 형태의 \( \vec{\theta} = {\theta_1, \dots, \theta_N} \)에 의해 결정된다고 가정해보자. 이때 MADDPG의 \(i\)번째 agent의 critic network는 centralized action-value function \( Q^\vec{\mu}_i(\vec{o}, a_1, \dots, a_N) \) 를 학습하게 되는데, 여기서 \( a_1 \in \mathcal{A}_1, \dots, a_N \in \mathcal{A}_N \)는 모든 agent의 action을 말한다. 각 \(Q_{i}^{\vec{\mu}}\) \(i=1, \dots, N\)으로 나누어져서 학습이 되는데, 이로 인해서 multiple agent는 서로 경쟁하는 형태의 conflicting reward를 포함하여, 하나의 reward 구조를 가지게 된다. 반면, 여러개의 actor network은 각 agent 별로 스스로 탐색하고, policy parameter \(\theta_{i}\)를 update하게 된다.
Actor Network update:
$$ \nabla_{\theta_{i}} J(\theta_{i}) = \mathbb{E}_{\vec{o}, a \sim D}[\nabla_{a_{i}} Q_{i}^{\vec{\mu}} ( \vec{o}, a_{1}, \dots, a_{N}) \nabla_{\theta_{i}} \mu_{\theta_{i}}(o_{i})|_{a_{i} = \mu_{\theta_{i}} (o_{i})} ] $$
위의 수식에서 \(D\)가 replay memory의 size라고 할 때, 해당 memory에 담겨있는 여러개의 episode sample은 \(( \vec{o}, a_{1}, \dots, a_{N}, r_{1}, \dots, r_{N}, \vec{o}') \) 이 될텐데, 이 표현의 의미는 주어진 현재의 observation \(\vec{o}\)이 있을 때, agent가 \(a_{1}, \dots, a_{N}\)에 해당하는 action을 수행하고 이에 따른 reward로 \( r_{1}, \dots, r_{N}\)을 받게 되며, 이로 인해서 새로운 observation \(\vec{o}'\)에 도달한다는 것이다.
Critic Network update:
$$ \begin{align} \mathcal{L}(\theta_{i}) &= \mathbb{E}_{\vec{o}, a_{1}, \dots, a_{N}, r_{1}, \dots, r_{N}, \vec{o}'}[ Q_{i}^{\vec{\mu}} (\vec{o}, a_{1}, \dots, a_{N}) - y )^{2} ] \\
\text{where } y &= r_{i} + \gamma Q_{i}^{\vec{\mu}'} (\vec{o}', a_{1}', \dots, a_{N}') |_{a_{j}' = \mu_{\theta_{j}}' } & \scriptstyle{\text{; TD target!}} \end{align}$$
위의 식에서 \( \vec{\mu}' \)은 delayed softly-updated parameter를 가진 target policy이다.
만약 target policy \( \vec{\mu}' \)가 critic network을 update하는 동안에 unknown 상태로 존재한다면, 각 agent로 하여금 이를 학습하고, 서로가 가지고 있는 policy에다가 어느정도의 approximation을 가해서 발전시킨다. MADDPG는 이렇게 각 agent별로 근사화된 policy들을 활용해서, output으로 도출한 policy가 그렇게 정확하지 않더라도 효율적으로 학습을 시킬 수 있게 된다.
물론 주어진 environment내에서 agent끼리 서로 경쟁하거나 협력을 하면서 high variance가 발생할 수 있는데, 이를 완화하기 위해서 MADDPG는 policy ensembles이라고 하는 요소를 하나 더 제안했다. 이 policy ensemble이 하는 역할은 다음과 같다.
- 한 개의 agent에 대해서 K개의 policy를 학습시킨다.
- episode rollout시 random하게 policy를 선택한다.
- policy들에 대한 gradient update를 수행하기 위해서 위의 K개의 policy에 대한 ensemble을 취한다.
간단하게 요약하자면, MADDPG는 multi-agent environment에서도 DDPG를 활용하기 위해서 DDPG에 다음 3개의 요소를 추가한 것이다.
- Centralized critic + decentralized actors의 형태
- Actor들은 policy learning을 위해서 다른 agent들이 가지고 있는 approximated policy를 활용할 수 있다.
- Variance를 줄이기 위해서 Policy ensemble을 가미했다.
TRPO (Trust Region Policy Optimization)
training stability를 향상시키기 위해서, 한 step내에서 policy를 변화시킬 수 있는 parameter update는 피해야 한다. Trust Region Policy Optimization (TRPO) (Schulman et al, 2015) 는 매 iteration 마다 policy를 update할 수 있는 size에 KL Divergence 제한을 가해서, parameter update를 피할 수 있게 했다.
만약 수행하는 policy가 off-policy라면, episode rollout이 behavior policy \( \beta(a|s)\) 를 따르는 동안의 objective function은 아래 식과 같이 주어진 모든 state visitation dstribution과 action에 대한 advantage를 계산하게 될 것이다.
$$ \begin{align} J(\theta) &= \sum_{s \in S} \rho^{\pi_{\theta_{\text{old}}}} \sum_{a \in A} \big( \pi_{\theta} (a|s) \hat{A}_{\theta_{\text{old}}}(s, a) \big) \\
&= \sum_{s \in S} \rho^{\pi_{\theta_{\text{old}}}} \sum_{a \in A} \big( \color{red}{\beta(a|s)} \frac{\pi_{\theta}(a|s)}{ \color{red}{ \beta(a|s)}} \hat{A}_{\theta_{\text{old}}}(s, a) \big) & \scriptstyle{ \text{; Applying Importance Sampling}} \\
&= \mathbb{E}_{s \sim \rho^{\pi_{\theta_{\text{old}}}}, \alpha \sim \beta} \big[ \frac{\pi_{\theta}(a|s)}{\beta(a|s)} \hat{A}_{\theta_{\text{old}}}(s, a) \big] \end{align}$$
위 식에서 \( \theta_{\text{old}} \)는 update 이전의 policy parameter이기 때문에, 우리가 알고 있는 값이고, \( \rho^{\pi_{\theta_{\text{old}}}} \) 는 DPG에서 구한 방식과 동일하게 정의할 수 있다. 그리고 \( \beta(a|s) \)는 수집된 trajectory에 대한 behavior policy이다. 여기서 우리는 보통 true reward에 대한 정보가 없기 때문에 true advantage function \( A(\cdot)\)가 아닌 estimated advantage function \( \hat{A}(\cdot)\)를 쓰게 된다.
위와 다르게 on-policy의 상황이라면, 이 때의 behavior policy \( \beta(a|s) \) 는 \( \pi_{\theta_{\text{old}}} (a|s) \)가 되고, 이 때의 objective function은 다음과 같이 된다.
$$ J(\theta) = \mathbb{E}_{s \sim \rho^{\pi_{\theta_{\text{old}}}}, a \sim \pi_{\theta_{\text{old}}}} \big[ \frac{\pi_{\theta}(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} \hat{A}_{\theta_{\text{old}}}(s, a) \big] $$
TRPO는 objective function \(J(\theta)\)를 최대화하는데 있어 trust region constraint를 사용했는데, 이건 KL-divergence에 의해서 측정되는 old policy와 new policy간의 간격을 작게 만들어주는 역할을 하고 보통 \(\delta \)로 표현된다.
$$ \mathbb{E}_{s \sim \rho^{\pi_{\theta_{\text{old}}}}} [ D_{KL} ( \pi_{\theta_{\text{old}}} (\cdot | s) || \pi_{\theta} (\cdot|s)] \le \delta $$
이 방법을 통해서, 이런 hard constraint가 충족되는 동안 old policy와 new policy가 그렇게 많이 diverge하지 않게 된다. 그러는 동안, TRPO는 policy iteration을 통해서 지속적인 성능 향상을 보여줄 수 있게 된다. 관심이 있으면 논문의 증명 부분을 읽어보면 좋을거 같다.
PPO ( Proximal Policy Optimization )
TRPO가 상대적으로 복잡하긴 하지만, 여전히 Trust Region Constraint와 유사한 constraint를 사용하고자 한다면, proximal policy optimization (PPO) (Schulman et al, 2017)는 clipped surrogate objective를 사용해서 TRPO와 유사한 성능을 내면서 이를 간단하게 만들 수 있다.
우선 old policy와 new policy 간의 probability ratio를 다음과 같이 정의하겠다.
$$ r(\theta) = \frac{\pi_{\theta}(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} $$
그러면 (on-policy) TRPO의 objective function은 다음과 같이 된다.
$$ J^{\text{TRPO}}(\theta) = \mathbb{E}[r(\theta) \hat{A}_{\theta_{\text{old}}}(s, a)] $$
\( \theta_{\text{old}} \)와 \(\theta\) 간의 거리에 대한 제한이 없다면, \(J^{\text{TRPO}}(\theta) \)를 maximize하는 작업 자체는 parameter update를 극도로 크게 만들수도 있고, policy ratio도 크게 만들만큼 안정성이 없게 된다. PPO에서는 \( r(\theta) \)가 1 이내의 작은 interval (정확하게는 \([1 - \epsilon, 1+ \epsilon] \) )내에 유지될 수 있게끔 constraint를 걸었는데, 여기서 \(\epsilon\)은 hyperparameter가 된다. (여기서 clip의 개념이 들어간다.)
$$ J^{\text{CLIP}}(\theta) = \mathbb{E}[ \min( r(\theta) \hat{A}_{\theta_{\text{old}}}(s, a), \text{clip}( r(\theta), 1 - \epsilon, 1+ \epsilon) \hat{A}_{\theta_{\text{old}}}(s, a)) ] $$
그래서 위의 식과 같이 Clip function이 적용된 objective function은 위와 같은데, 여기서 \( \text{clip}( r(\theta), 1 - \epsilon, 1+ \epsilon) \)은 \( [ 1 - \epsilon, 1 + \epsilon ] \) 내에서 ratio을 다듬는(clip) 역할을 한다. 그래서 PPO의 objective function은 원래의 값과 clip된 값들 중 작은 값을 취하는 형태로 되어 있는데, 이를 통해서 좀더 나은 reward를 얻기 위해서 극도로 policy를 update하는 등의 동작은 없어지게 된다.
policy fuction (actor)와 value function (critic)간에 parameter를 공유하는 형태의 network에다가 PPO를 적용하는 경우, 앞에서 소개한 clipped reward를 쓰는 것에 덧붙여서, objective function에다가 value estimation에 대한 error term (아래 식 중 빨간 부분) 와 entropy term (아래 식 중 파란 부분)을 덧붙여서 사용하는데, 이를 통해 exploration을 충분히 수행할 수 있도록 해준다.
$$ J^{\text{CLIP}'}(\theta) = \mathbb{E}[ J^{\text{CLIP}}(\theta) - \color{red}{ c_{1}( V_{\theta}(s) - V_{\text{target}})^{2}} + \color{blue}{ c_{2} H(s, \pi_{\theta}(\cdot))}] $$
여기서도 역시 \(c_{1}, c_{2} \)는 hypterparameter constant이다.
PPO는 여러 benchmark task에서도 훨씬 더 간단하면서도, 놀라운 결과를 보여줬다.
ACER ( Actor-Critic with Experience Replay )
ACER는 Actor-Critic with Experience Replay (Wang et al, 2017) 를 줄인 말로, experience replay를 가진 off-policy actor-critic 모델이며, sample efficiency를 많이 향상시키고, data correlation을 줄였다. A3C가 ACER의 기반이긴 하지만, on-policy 였고, ACER가 A3C의 off-policy 모델이라고 보면 될거 같다. A3C를 off-policy 형태로 만드는데 있어 가장 큰 걸림돌은 off-policy estimator에 대한 stability를 어떻게 제어할 수 있느냐였다. ACER는 이를 극복하기 위해서 3가지 개선 사항을 적용했다.
- Retrace Q-value estimation 적용
- bias correction을 통해서 importance weight를 생략함
- efficient TRPO 적용
Retrace Q-Value Estimation
Retrace 는 off-policy return 기반의 Q-value estimation 알고리즘으로, 어떤 target policy 와 behavior policy ( \( \pi, \beta \) ) 에 대해서도 convergence를 보장하고, 추가로 data efficiency까지 가져왔다.
잠시 prediction을 위한 TD learning이 어떻게 동작하는지를 살펴보자.
- TD error 를 계산한다. ( \( \delta_{t} = R_{t} + \gamma \mathbb{E}_{a \sim \pi} Q(S_{t+1}, a) - Q(S_{t}, A_{t}) \))
여기서 \( r_{t} + \gamma \mathbb{E}_{a \sim \pi} Q(s_{t+1}, a) \)는 "TD target"으로 알려져 있는 부분이다. 그리고 expectation \( \mathbb{E}_{a \sim \pi} \) 를 취하는 이유는 현재의 policy \( \pi \)를 취할 때, total return이 어떻게 될지에 대한 가장 좋은 estimation이기 때문이다. - goal에 도달하기 위해서 error를 수정하면서 Q-value를 update함 ( \(Q(S_{t}, A_{t}) \leftarrow Q(S_{t}, A_{t}) + \alpha \delta_{t} \) )
다르게 표현하면 Q-value에 대한 증가폭은 TD error에 비례하다는 것이다. ( \( \Delta Q(S_{t}, A_{t}) = \alpha \delta_{t} \) )
rollout이 off-policy일 경우, Q-value update할때 importance sampling을 적용해야 한다.
$$ \Delta Q^{\text{imp}}(S_{t}, A_{t}) = \gamma^{t} \prod_{1 \leq \tau \leq t} \frac{\pi(A_{\tau}| S_{\tau})}{\color{red}{\beta(A_{\tau}|S_{\tau})}} \delta_{t} $$
importance weight로 product를 취하는 것은 어쩌면 이로 인해 엄청 큰 variance를 야기할 수도 있기 때문에 고민이 되는 부분이다. Retrace Q-value estimation은 importance weight가 상수 c 이상보다 커질 수 없도록 \( \Delta Q \)를 수정하는 방법을 취했다.
$$ \Delta Q^{\text{ret}}(S_{t}, A_{t}) = \gamma^{t} \prod_{1 \leq \tau \leq t} \min (\color{red}{c}, \frac{\pi(A_{\tau}|S_{\tau})}{\beta(A_{\tau} | S_{\tau})}) \delta_{t} $$
ACER에서는 L2 Error term( \( \big( Q^{\text{ret}}(s,a) - Q(s, a) \big)^{2} \) ) 을 최소화함으로써 critic network을 학습시킬 때, 모델이 지향해야 할 target model을 계산하기 위해 \( Q^{\text{ret}} \) 을 사용했다.
Importance weights truncation
policy gradient \( \hat{g} \)의 high variance 현상을 줄이기 위해서, ACER에서는 importance weight를 상수 c로 제한을 걸고, 여기에 덧붙여 correction term을 추가했다. 아래의 식에 나오는 \( \hat{g}_{t}^{\text{ACER}} \) 가 바로 \(t\)시점에서의 ACER policy gradient를 나타낸다.
$$ \begin{align} \hat{g}_{t}^{\text{ACER}} &= w_{t} \big( Q^{\text{ret}}(S_{t}, A_{t}) - V_{\theta_{v}}(S_{t})\big) \nabla_{\theta} \ln \pi_{\theta} (A_{t}|S_{t}) & \scriptstyle{ \text{; Let } w_{t} = \frac{\pi(A_{t}|S_{t})}{\beta(A_{t}|S_{t}))}} \\
&= \color{blue}{\min (c, w_{t}) \big( Q^{\text{ret}} (S_{t}, A_{t}) - V_{w}(S_{t})\big) \nabla_{\theta} \ln \pi_{\theta}(A_{t}|S_{t})} \\ &+ \color{red}{\mathbb{E}_{a \sim \pi} [ \max (0, \frac{w_{t}(a) - c}{w_{t}(a)}) \big( Q_{w}(S_{t}, a) - V_{w}(S_{t}) \big) \nabla_{\theta} \ln \pi_{\theta}(a|S_{t})]} & \scriptstyle{ \text{; Let } w_{t}(a) = \frac{ \pi(a|S_{t})}{ \beta(a|S_{t})} } \end{align} $$
여기서 \(Q_{w}(\cdot)\)과 \( V_{w}(\cdot)\)은 parameter \(w\)에 따라서 critic network가 predict 하는 value function이 되고, 식 첫째줄의 \( V_{\theta_{v}}(S_{t}) \)은 variance를 줄이기 위해서 설정한 classic baseline이다. 우선 두번째 식의 첫번째 항(파란 부분)은 clipped importance weight인데, 이렇게 clipping 기법을 적용하면 variance를 낮추는데 도움이 된다. 여기다가 baseline인 state-value function \(V_{w}(\cdot)\)를 빼서 variance reduction 효과를 더 높일 수 있게 된다. 두번째 항(빨간 부분)은 앞에서 소개했다시피 unbiased estimation을 얻기 위해서 correction term을 삽입한 것이다.
Efficient TRPO
추가적으로, ACER는 TRPO의 개념에다 연산을 효율적으로 처리하기 위해서 수정을 약간 가했다. TRPO에서는 한 update 시점을 기준으로 이전의 policy와 이후의 policy 사이의 KL divergence를 계산했었는데, ACER는 이전의 policy에 대한 average를 유지하고, update되는 policy가 이 average에서 그렇게 멀어지지 않게끔 제한을 두었다.
ACER 논문은 수많은 공식들로 꽉차있는 논문이기 때문에 TD-learning이나 Q-learning, importance sampling, TRPO에 대한 지식을 가지고 본다면 조금더 쉽게 이해할 수 있을 것이다.
ACKTR (Actor-Critic using Kronecker-factored Trust Region)
ACKTR (Actor-Critic using Kronecker-factored Trust Region) (Yuhuai et al, 2017) (actor의 발음과 유사) 는 Actor-critic 모델에서 각 network가 gradient update를 할 때 Kronecker-factored approximation curvature (K-FAC)를 쓰는 것을 제안했다. K-FAC은 natural gradient를 연산하는데 있어 큰 개선점을 가져왔는데, 여기서 natural gradient는 우리가 알고 있는 standard gradient와는 조금 다른 개념이다. 여기에 natural gradient에 대해서 설명을 잘해놓은 곳이 있는데, 요약을 다음과 같이 하고 있었다.
"우선 old network에 대해서 new network의 KL Divergence의 constant 값을 얻을 수 있는 모든 parameter의 조합을 고려했다. 이 constant 값은 step size나 learning rate 관점으로도 바라볼 수 있는데, 이런 parameter 조합들중에서 loss function을 최소화할 수 있는 것을 선택하는 것이 natural gradient의 의미이다."
우선 여기에선 ACTKR를 소개했지만, 여기에는 natural gradient과 optimization method에 대한 수많은 이론적 개념이 관련되어 있기 때문에, 자세히 다루지는 않을 것이다. 혹시 이 개념에 관심이 있다면, ACKTR 논문을 읽기 전에 아래 글들을 읽어볼 것을 권한다.
- Amari, Natural Gradient Works Efficiently in Learning, 1998
- Kakade, A Natural Policy Gradient, 2002
- A intuitive explanation of natural gradient descent
- (Wikipedia) Kronecker product
- Martens & Grosse, Optimizing neural networks with kronecker-factored approximate curvature, 2015
여기 K-FAC 논문에 대한 요약을 나열했다.
"여기에 나온 Approximation은 크게 두가지 과정으로 나누어져 있다. 첫번째로 Fisher information의 row와 column을 그룹별로 나누는데, 각 그룹은 주어진 layer에 대한 모든 weights를 나타내게끔 되고, 이 값들이 결국 matrix에 대한 block-partitioning을 야기하게 된다. 그러면 해당 group내의 block들은 훨씬 작은 행렬들 사이의 Kronecker product로 approximate시킬 수 있게 된다. 여기서 우리가 확인하고 싶은 부분은 해당 network의 gradient에 대한 statistics와 관련하여 assumption을 추정할 수 있는 무언가가 있느냐는 것이다.
두번째 단계에서는 이 행렬을 block-diagonal하거나 block-tridiagonal 한 inverse matrix로 approximate하는 것이다. 여기서 도출되는 approximation은 inverse covariance와 tree-structured graphic model, 그리고 linear regression 사이의 관계를 잘 살펴봄으로써 증명할 수 있다. 확실한 것은 이런 증명은 Fisher information 자체에 적용하는 것이 아니라는 것인데, 실험을 통해서 inverse fisher information이 이런 구조를 (approximate하게) 가지고는 있지만, Fisher information 자체는 그런 구조를 가지지 않는다는 것을 확인할 수 있었다."
SAC (Soft Actor-Critic)
Soft Actor-Critic (SAC) (Haarnoja et al, 2018) 는 exploration을 조금더 잘하게 하기 위해서 reward에다가 policy에 대한 entropy measure를 추가한 기법이다. 이를 통해서 가능한한 랜덤하게 행동하면서, task를 잘 수행할 수 있게끔 policy를 학습하길 바라는 것이다. 이 기법은 off-policy actor-critic model에 maximum entropy reinforcement learning framework를 가미한 것이다. 이전에는 Soft Q-learning 이란 이름으로 연구가 진행되었었다.
SAC를 구성하는 3가지 요소는 다음과 같다.
- policy function network와 value function network을 따로 분리해서 가지고 있는 actor-critic 구조
- 이전에 수집한 data를 재사용할 수 있는 형태의 off-policy formulation
- Stability와 exploration을 만족시키기 위한 Entropy maxmization
Policy는 동시에 entropy와 expected return을 최대화하기 위한 objective function을 통해서 학습된다.
$$ J(\theta) = \sum_{t=1}^{T} \mathbb{E}_{(s_{t}, a_{t}) \sim \rho_{\pi_{}\theta}} [ r(s_{t}, a_{t}) + \alpha \mathcal{H}(\pi_{\theta}(\cdot | s_{t}))] $$
위 식에서 \( \mathcal{H}(\cdot)\)이 entropy measure이고, \( \alpha \)는 entropy term의 중요성을 결정하는 변수로 보통은 temperature parameter로 알려져 있다. 여기서 Entropy maximization을 통해 policy가 (1) 조금더 탐색하고 (2) near-optimal strategy들의 여러가지 형태를 담을 수 있게끔 해준다. (예를 들어 똑같이 좋아보이는 option들이 여러개 존재한다면, policy는 동일한 확률로 해당 option을 선택할 수 있어야 한다는 것이다.)
결국 SAC는 세가지 함수를 학습하는데 초점을 맞추고 있다.
- Parameter \( \theta \)에 대한 policy, \( \pi_{\theta} \)
- Parameter \( w\)에 의해 결정되는 Soft Q-value function, \( Q_{w} \)
- Parameter \( \psi \)에 의해 결정되는 Soft state-value function, \( V_{\psi} \)
: 이론적으로는 \(Q\)와 \( \pi \)를 통해서 \(V\)를 추론할 수 있지만, 실제 상황에서는 이렇게 하면 training에 안정성을 더할 수 있다.
Soft Q-value (아니면 state-action value) 와 soft state value는 다음과 같이 정의할 수 있다
$$ \begin{align} Q(s_{t}, a_{t}) &= r(s_{t}, a_{t}) + \gamma \mathbb{E}_{ s_{t+1} \sim \rho_{\pi}(s)} [V(s_{t+1})] & \scriptstyle{\text{; according to Bellman equation}} \\
\text{where } V(s_{t}) &= \mathbb{E}_{a_{t} \sim \pi} [ Q(s_{t}, a_{t}) - \alpha \log \pi (a_{t} | s_{t})] & \scriptstyle{\text{; soft state value function}} \end{align} $$
여기서 Q-value내의 \( V(s_{t+1})\)을 state value function으로 치환시키면 아래 식과 같이 유도할 수 있다.
$$ Q(s_{t}, a_{t}) = r(s_{t}, a_{t}) + \gamma \mathbb{E}_{ (s_{t+1}, a_{t+1}) \sim \rho_{\pi}} [ Q(s_{t+1}, a_{t+1}) - \alpha \log \pi (a_{t+1} | s_{t+1})] $$
여기서 \( \rho_{\pi}(s) \)와 \( \rho_{\pi}(s, a) \)는 policy \( \pi(a|s) \)에 의해서 도출되는 state distribution의 state marginal과 state-action marginal 인데, 이 부분은 DPG에서도 비슷한 방식으로 유도했었다.
soft state value function은 mean squared error를 최소화하는 방향으로 학습된다.
$$ \begin{align} J_{V}(\psi) &= \mathbb{E}_{s_{t} \sim D} [\frac{1}{2} \big( V_{\psi}(s_{t}) - \mathbb{E} [Q_{w}(s_{t}, a_{t}) - \log \pi_{\theta} (a_{t} | s_{t})] \big)^{2}] \\
\text{with gradient: } \nabla_{\psi} J_{V}(\psi) &= \nabla_{\psi} V_{\psi}(s_{t}) \big( V_{\psi}(s_{t}) - Q_{w}(s_{t}, a_{t}) + \log \pi_{\theta} (a_{t} | s_{t}) \big) \end{align} $$
위의 식에서 \(D \)은 replay buffer를 말한다.
soft Q function은 soft Bellman residual을 최소화하는 방향으로 학습된다.
$$ \begin{align} J_{Q}(w) &= \mathbb{E}_{(s_{t}, a_{t}) \sim D} [\frac{1}{2} \big( Q_{w}(s_{t}, a_{t}) - (r(s_{t}, a_{t}) + \gamma \mathbb{E}_{s_{t+1} \sim \rho_{\pi}(s)} [V_{\bar{\psi}}(s_{t+1})] \big)^{2}] \\
\text{with gradient: } \nabla_{w} J_{Q}(w) &= \nabla_{w} Q_{w}(s_{t}, a_{t}) \big( Q_{w}(s_{t}, a_{t}) - r(s_{t}, a_{t}) - \gamma V_{\bar{\psi}}(s_{t+1}) \big) \end{align} $$
잘 보일지는 모르겠지만 \( \bar{\psi} \)는 exponential moving average를 가지는 (혹은 "어려운 방법으로" 주기적으로만 update되는 ) target value function을 말하는데, 마치 DQN에서 training을 안정화시키기 위해서 target Q network의 parameter를 다루는 방법과 동일하다.
SAC는 KL-divergence를 최소화하는 방향으로 policy를 update한다.
$$ \begin{aligned}
\pi_\text{new}
&= \arg\min_{\pi' \in \Pi} D_\text{KL} \Big( \pi'(.\vert s_t) \| \frac{\exp(Q^{\pi_\text{old}}(s_t, .))}{Z^{\pi_\text{old}}(s_t)} \Big) \\[6pt]
&= \arg\min_{\pi' \in \Pi} D_\text{KL} \big( \pi'(.\vert s_t) \| \exp(Q^{\pi_\text{old}}(s_t, .) - \log Z^{\pi_\text{old}}(s_t)) \big) \\[6pt]
\text{objective for update: } J_\pi(\theta) &= \nabla_\theta D_\text{KL} \big( \pi_\theta(. \vert s_t) \| \exp(Q_w(s_t, .) - \log Z_w(s_t)) \big) \\[6pt]
&= \mathbb{E}_{a_t\sim\pi} \Big[ - \log \big( \frac{\exp(Q_w(s_t, a_t) - \log Z_w(s_t))}{\pi_\theta(a_t \vert s_t)} \big) \Big] \\[6pt]
&= \mathbb{E}_{a_t\sim\pi} [ \log \pi_\theta(a_t \vert s_t) - Q_w(s_t, a_t) + \log Z_w(s_t) ]
\end{aligned} $$
위의 식에서 policy \( \Pi \)는 현재의 policy를 가지고 쉽게 바꿀수 있는 잠재적인 policy들의 집합이다. 예를 들어 \( \Pi \)는 modeling하기는 어렵지만, 직관적이고, 쉽게 다룰 수 있는 Gaussian mixture distribution의 집합일 수도 있다. \(Z^{\pi_{\text{old}}}(s_{t}) \)는 distribution을 normalize시키는 partition function이다. 이건 쉽게 다룰수 있는건 아니지만 그렇다고 gradient에 영향을 미치는 것은 아니다. 결국 objective function인 \( J_{\pi}(\theta) \)를 최소화하는 것은 policy들의 집합인 \( \Pi \)를 어떻게 선택하냐에 달린 것이다.
이렇게 update를 하면서 \( Q^{\pi_{\text{new}}} (s_{t}, a_{t}) \ge Q^{\pi_{\text{old}}} (s_{t}, a_{t}) \)의 관계는 항상 만족시키는데, 이 부분에 대한 증명은 논문의 Appendix B.2의 lemma를 살펴보면 확인할 수 있다.
한번 이렇게 soft action-state value, soft state value network, policy network에 대해서 objective function 과 gradient가 정의되면, soft actor-critic algorithm은 직관적으로 표현할 수 있게 된다.

SAC with Automatically Adjusted Temperature
SAC algorithm은 temperature parameter와 관련해서는 불안한 성향을 띈다. 사실 entropy 자체가 더 좋은 policy를 찾는 목적을 가진 상태에서 task를 수행하거나 학습하는 순간 모두 매우 예측이 어렵기 때문에, temperature를 조절하는 것 자체가 어렵긴 하다. 그래서 SAC에서 개선점을 찾은 것은 제한된(constrained) optimization problem을 사용하자는 것이다. 다시 말하자면, expected return을 최적화하면서, policy가 아래의 minimum entropy constraint를 만족시키게끔 하자는 것이다.
$$ \max_{\pi_{0}, \dots ,\pi_{T}} \mathbb{E} \Big[ \sum_{t=0}^{T} r(s_{t}, a_{t}) \Big] \text{s.t. } \forall t\text{, } \mathcal{H}(\pi_{t}) \geq \mathcal{H}_{0} $$
위 식에서 \( \mathcal{H}_{0} \)은 미리 정의한 minimum policy entropy threshold 이다.
Expected return \( \mathbb{E} \Big[ \sum_{t=0}^{T} r(s_{t}, a_{t}) \Big] \) 은 모든 time step 에 대한 reward들의 합으로 나눠서 볼 수 있다. 사실 policy \(\pi_{t} \)는 이전 time step의 policy \( \pi_{t-1} \)에는 전혀 영향을 주지 않기 때문에, 정해진 time step \(T\)에 대해서 서로 다른 step size로 나누어서 return maximize할 수 있게 된다. (어떻게 보면 이건 Dynamic Programming이기도 하다.)
일단 \( \gamma = 1 \)이라고 가정하면 위의 문제는 아래와 같이 재정의를 할 수 있다.
$$ \underbrace{\max_{\pi_0} \Big( \mathbb{E}[r(s_0, a_0)]+ \underbrace{\max_{\pi_1} \Big(\mathbb{E}[...] + \underbrace{\max_{\pi_T} \mathbb{E}[r(s_T, a_T)]}_\text{1st maximization} \Big)}_\text{second but last maximization} \Big)}_\text{last maximization} $$
그러면 가장 마지막 time step \(T\)에서부터 optimization을 수행할 수 있다.
$$ \text{maximize } \mathbb{E}_{(s_{T}, a_{T}) \sim \rho_{\pi}} [r(s_{T}, a_{T})] \text{ s.t. } \mathcal{H}(\pi_{T}) - \mathcal{H}_{0} \ge 0 $$
여기서 다음의 함수를 만들게 되면,
$$ \begin{align} h(\pi_{T}) &= \mathcal{H}(\pi_{T}) - \mathcal{H}_{0} = \mathbb{E}_{(s_{T}, a_{T}) \sim \rho_{\pi}} [ - \log \pi_{T} (a_{T} | s_{T})] - \mathcal{H}_{0} \\
f(\pi_{T}) &= \begin{cases} \mathbb{E}_{(s_{T}, a_{T}) \sim \rho_{\pi}} [r(s_{T}, a_{T})], & \text{if } h(\pi_{T}) \ge 0 \\
-\infty & \text{otherwise} \end{cases} \end{align} $$
optimization은 다음과 같이 축약할 수 있게 된다.
$$ \text{maximize} f(\pi_{T}) \text{ s.t. } h(\pi_{T}) \ge 0 $$
위와 같은 inequality constraint를 가진 상태에서의 maximization optimization을 풀기 위해서는 Lagrange multiplier ("dual variable"라고도 부르는 것) \( \alpha_{T} \)를 이용한 Lagrangian expression을 만들어야 한다.
$$ L(\pi_{T}, \alpha_{T}) = f(\pi_{T}) + \alpha_{T} h(\pi_{T}) $$
특정한 policy \( \pi_{T}\)가 주어졌을 때 \( \alpha_{T} \)에 관해서 \( L(\pi_{T}, \alpha_{T}) \)를 최소화하는 case를 고려해보면 다음과 같다.
- \( h(\pi_{T}) \ge 0 \)와 같이 Constraint가 만족될 경우, \( f(\pi_{T}) \)의 값에 대해서 조절할 수 없기 때문에 \( \alpha_{T} = 0 \)라고 설정할 수 있고, 이로 인해 Lagrangian Expression은 다음과 같이 \(L(\pi_{T}, 0) = f(\pi_{T}) \)라고 정의할 수 있다.
- 만약 constraint가 충족되지 않는다면, 결국 \(h(\pi_{T}) \lt 0 \) 이므로, \(\alpha_{T} \to \infty \)를 취함으로써, \(L(\pi_{T}, \alpha_{T}) \to - \infty \)라는 관계를 얻을 수 있다. 이로 인해 Lagrangian Expression은 \( L(\pi_{T}, \infty) = - \infty = f(\pi_{T}) \)라고 정의할 수 있다.
위의 두가지 case 모두 다음의 equatoin을 정의할 수 있고,
$$ f(\pi_{T}) = \min_{ \alpha_{T} \ge 0 } L(\pi_{T}, \alpha_{T}) $$
동시에 이 \(f(\pi_{T})\)를 maximize해야 한다.
$$ \max_{\pi_{T}} f(\pi_{T}) = \min_{\alpha_{T} \ge 0} \max_{\pi_{T}} L(\pi_{T}, \alpha_{T}) $$
결국, \(f(\pi_{T})\)를 maximize하기 위해서는 dual problem을 아래와 같이 나열해볼 수 있다. 기억해야 할 것은 \( \max_{\pi_{T}} f(\pi_{T})\)를 확실하게 maximize하고, \( -\infty \) 가 되지 않게끔 하고 싶을 경우, constraint는 항상 만족되어야 한다는 것이다.
$$ \begin{align} \max_{\pi_{T}} \mathbb{E} [r(s_{T}, a_{T}) &= \max_{\pi_{T}} f(\pi_{T})] \\
&= \min_{\alpha_{T} \ge 0} \max_{\pi_{T}} L(\pi_{T}, \alpha_{T}) \\
&= \min_{\alpha_{T} \ge 0} \max_{\pi_{T}} f(\pi_{T}) + \alpha_{T}h(\pi_{T}) \\
&= \min_{\alpha_T \geq 0} \max_{\pi_T} \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi}} [ r(s_T, a_T) ] + \alpha_T ( \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi}} [-\log \pi_T(a_T\vert s_T)] - \mathcal{H}_0) \\
&= \min_{\alpha_T \geq 0} \max_{\pi_T} \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi}} [ r(s_T, a_T) - \alpha_T \log \pi_T(a_T\vert s_T)] - \alpha_T \mathcal{H}_0 \\
&= \min_{\alpha_T \geq 0} \max_{\pi_T} \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi}} [ r(s_T, a_T) + \alpha_T \mathcal{H}(\pi_T) - \alpha_T \mathcal{H}_0 ] \end{align}$$
이제 optimal \( \pi_{T}\) 와 \( \alpha_{T} \)를 순차적으로 계산하려고 한다. 우선, 주어진 현재의 \( \alpha_{T} \)에 대해서 \(L( \pi_{T}^{*}, \alpha_{T}) \)를 maximize할 수 있는 best policy \( \pi_{T}^{*} \)를 구한다. 그리고 난 후 policy \( \pi_{T}^{*} \)를 대입해서 \( L( \pi_{T}^{*}, \alpha_{T}^{*}) \) 를 minimize할 수 있는 \( \alpha_{T}^{*} \)를 구한다. 만약 policy를 구하기 위한 neural network 한개와 temperature parameter를 구하기 위한 neural network을 하나 가지고 있다고 가정해보면, 이런 순차적인 update process는 training동안 network parameter를 update하는 방법과 동일하게 된다.
$$ \begin{align} \pi^{*}_T
&= \arg\max_{\pi_T} \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi}} [ r(s_T, a_T) + \alpha_T \mathcal{H}(\pi_T) - \alpha_T \mathcal{H}_0 ] \\
\color{blue}{\alpha^{*}_T}
&\color{blue}{=} \color{blue}{\arg\min_{\alpha_T \geq 0} \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi^{*}}} [\alpha_T \mathcal{H}(\pi^{*}_T) - \alpha_T \mathcal{H}_0 ]}\end{align} $$
$$ \text{Thus, }\max_{\pi_T} \mathbb{E} [ r(s_T, a_T) ]
= \mathbb{E}_{(s_T, a_T) \sim \rho_{\pi^{*}}} [ r(s_T, a_T) + \alpha^{*}_T \mathcal{H}(\pi^{*}_T) - \alpha^{*}_T \mathcal{H}_0 ] $$
그럼 이제 다시 soft Q-value function을 살펴보면, 다음과 같다.
$$ \begin{align} Q_{T-1}(s_{T-1}, a_{T-1}) &= r(s_{T-1}, a_{T-1}) + \mathbb{E} [ Q(s_{T}, a_{T}) - \alpha_{T} \log \pi (a_{T} | s_{T})] \\
&= r(s_{T-1}, a_{T-1}) + \mathbb{E} [ r(s_{T}, a_{T}) ] + \alpha_{T} \mathcal{H}(\pi_{T}) \\
Q_{T-1}^{*} (s_{T-1}, a_{T-1}) &= r(s_{T-1}, a_{T-1}) + \max_{\pi_{T}} \mathbb{E}[r(s_{T}, a_{T}] + \alpha_{T} \mathcal{H}( \pi_{T}^{*}) & \scriptstyle{ \text{; plug in the optimal } \pi_{T}^{*} } \end{align} $$
그러면 time step \( T-1 \)으로 돌아갔을때의 expected return은 다음과 같이 된다.
$$ \begin{aligned}
&\max_{\pi_{T-1}}\Big(\mathbb{E}[r(s_{T-1}, a_{T-1})] + \max_{\pi_T} \mathbb{E}[r(s_T, a_T] \Big) \\
&= \max_{\pi_{T-1}} \Big( Q^{*}_{T-1}(s_{T-1}, a_{T-1}) - \alpha^{*}_T \mathcal{H}(\pi^{*}_T) \Big) & \text{; should s.t. } \mathcal{H}(\pi_{T-1}) - \mathcal{H}_0 \geq 0 \\
&= \min_{\alpha_{T-1} \geq 0} \max_{\pi_{T-1}} \Big( Q^{*}_{T-1}(s_{T-1}, a_{T-1}) - \alpha^{*}_T \mathcal{H}(\pi^{*}_T) + \alpha_{T-1} \big( \mathcal{H}(\pi_{T-1}) - \mathcal{H}_0 \big) \Big) & \text{; dual problem w/ Lagrangian.} \\
&= \min_{\alpha_{T-1} \geq 0} \max_{\pi_{T-1}} \Big( Q^{*}_{T-1}(s_{T-1}, a_{T-1}) + \alpha_{T-1} \mathcal{H}(\pi_{T-1}) - \alpha_{T-1}\mathcal{H}_0 \Big) - \alpha^{*}_T \mathcal{H}(\pi^{*}_T)
\end{aligned} $$
그러면 이전의 time step \(T\)와 동일한 방법으로 optimal policy \( \pi_{T-1}^{*} \)와 \( \alpha_{T-1}^{*} \)을 구해볼 수 있다.
$$ \begin{aligned}
\pi^{*}_{T-1} &= \arg\max_{\pi_{T-1}} \mathbb{E}_{(s_{T-1}, a_{T-1}) \sim \rho_\pi} [Q^{*}_{T-1}(s_{T-1}, a_{T-1}) + \alpha_{T-1} \mathcal{H}(\pi_{T-1}) - \alpha_{T-1} \mathcal{H}_0 ] \\
\color{green}{\alpha^{*}_{T-1}} &\color{green}{=} \color{green}{\arg\min_{\alpha_{T-1} \geq 0} \mathbb{E}_{(s_{T-1}, a_{T-1}) \sim \rho_{\pi^{*}}} [ \alpha_{T-1} \mathcal{H}(\pi^{*}_{T-1}) - \alpha_{T-1}\mathcal{H}_0 ]}
\end{aligned} $$
초록색으로 표현한 \( \alpha_{T-1} \)을 update하는 공식은 위에서 파란색으로 표현한 \( \alpha_{T} \)를 update하는 공식과 동일한 형태를 가지고 있는 것을 확인할 수 있다. 이런 과정을 반복해서, 아래와 같은 동일한 objective function을 minimize함으로써, 매 time step 마다 optimal temperature parameter를 학습할 수 있게 된다.
$$ J(\alpha) = \mathbb{E}_{a_{t} \sim \pi_{t}}[ - \alpha \log \pi_{t} (a_{t} | \pi_{t}) - \alpha \mathcal{H}_{0}] $$
objective function \( J(\alpha) \)에 관하여 \( \alpha \)를 학습하는 것을 제외하고 나머지 부분은 SAC algorith과 동일하다.

TD3 (Twin Delayed Deep Deterministic Policy Gradient)
Q-learning algorithm은 흔히 value function에 대한 overestimation으로 인한 성능의 영향을 받는 것으로 알려져 있다. 이렇게 overestimation이 training 도중에 계속 발생하면, policy update시 부정적으로 영향을 끼치게 된다. 이런 특성으로 인해서 Double Q-learning과 Double DQN이란 기법들이 등장했는데, 이 두가지 방법은 두개의 value network을 사용해서 action selection update와 Q-value update를 분리시키는 방법이었다.
Twin Delayed Deep Deterministic Policy Gradient (TD3; Fujimoto et al, 2018)는 이렇게 value function에 대한 overestimation을 막기 위해서 DDPG에다가 몇가지 기법을 적용한 algorithm이다.
(1) Clipped Double Q-learning : Double Q-learning에서는 action selection과 Q-value estimation이 두개의 network으로 따로 분리되어 이뤄졌었다. DDPG 설정에 맞췄을때, 두개의 deterministic actor network ( \(\mu_{\theta_{1}}, \mu_{\theta_{2}} \) )와 두개의 critic network ( \( Q_{w_{1}}, Q_{w_{2}} \) )이 있는 상태에서 Double Q-learning의 Bellman equation은 다음과 같이 도출할 수 있다.
$$ \begin{align} y_{1} &= r + \gamma Q_{w_{2}}(s', \mu_{\theta_{1}}(s')) \\
y_{2} &= r + \gamma Q_{w_{1}} (s', \mu_{\theta_{2}}(s')) \end{align} $$
하지만, policy가 느리게 변화하기 때문에, 서로 independent한 decision을 하기에는 두개의 network가 너무 유사하게 된다. 이를 피하기 위해, Clippped Double Q-learning은 두 network 중 minimum estimation을 선택하게끔 해서 학습 도중에 벗어나는 것을 막는 underestimation bias를 선호하게 만들었다.
$$ \begin{align} y_{1} &= r + \gamma \min_{i=1, 2} Q_{w_{i}} (s', \mu_{\theta_{1}}(s')) \\
y_{2} &= r+ \gamma \min_{i=1, 2} Q_{w_{i}} (s', \mu_{\theta_{2}}(s')) \end{align} $$
(2) Delayed update of Target and Policy Networks : actor-critic 모델에서는, policy network의 update와 value network의 update가 깊게 연관되어 있는데, 다시 말해서 policy network이 나쁘게 동작하면, overestimation에 의해서 Value estimation diverge하고, value network이 부정확하면, policy network 자체도 나쁘게 된다는 것이다.
결국 Variance를 줄이기 위해서, TD3는 policy network를 Q-function보다는 적은 빈도로 update시킨다. Policy network은 value error가 update동안 충분히 작아질 때까지 그대로 유지하게 되는 것이다. 이런 개념은 DQN에서 target network이 stable objective function을 가진 상태로 주기적으로 update하는 방법과 유사하다.
(3) Target Policy Smoothing : value function에서 아주 잠깐 발생하는 peak에 의해서 overfit 될 수 있는 deterministic policy에 대처하기 위해서, TD3는 value function에 대한 smoothing regularization strategy를 적용했다. 이 때 뽑혀진 action에 대해서 작은 clipped random noise를 가하고, mini-batch 내에서 평균을 취하는 것이다.
$$ \begin{aligned}
y &= r + \gamma Q_w (s', \mu_{\theta}(s') + \epsilon) & \\
\epsilon &\sim \text{clip}(\mathcal{N}(0, \sigma), -c, +c) & \scriptstyle{\text{ ; clipped random noises.}}
\end{aligned} $$
(중간의 \( \mathcal{N}(0, \sigma) \)는 통계에서 나오는 내용이지만, mean이 0이고 standard deviation이 \(\sigma\)인 normal distribution을 나타내는 것이다.)
이런 접근 방식은 SARSA algorithm의 update 방식에서 차용해온 것이고, 이를 통해서 서로 유사한 action은 유사한 value를 가지게끔 해준다.
이게 최종 algorithm이다.

Quick Summary
위의 algorithm을 다뤄본 후에, algorithm 사이에 공통되는 요소나 원칙에 대해서 나열해보고자 한다.
- 학습을 stabilize하기 위해서는 variance를 줄이고, bias가 변하지 않게끔 유지시켜라
- Off-policy 기법은 exploration을 더 잘할 수 있게 해주고, data sample을 효율적으로 사용할 수 있게 해준다.
- Experience Replay 사용 (replay memory buffer로부터 data를 sampling해서 학습시킴)
- Target network은 Actively learned policy network보다는 느리게 update되거나, 주기적으로 고정된다.
- Batch Normalization 적용
- Entropy-regularized reward 사용
- Critic Network와 Actor Network은 서로 network내의 하위 계층의 parameter와 policy function과 value function을 대표하는 두개의 output을 공유할 수 있다.
- Stochastic Policy가 아닌 Deterministic Policy를 학습시키는 것도 가능하다.
- Policy update시 policy가 diverge하는 것을 막기 위한 Constraint를 삽입한다.
- (K-FAC과 같은) 새로운 optimization method를 적용해볼 수 있다.
- Policy에 대한 Entropy Maximization은 Agent가 exploration을 더 잘할 수 있게끔 해준다.
- Value function에 대한 overestimation이 발생하지 않도록 해라.
- 그외 다른 것들도 있겠다.
(역자) 긴 페이지를 할애하여 Policy Gradient에 대한 정리를 했다. 개인적으로 강화학습을 공부하는 입장에서 Policy Gradient method들을 review하다보니, 정말로 많은 수식 증빙과 이론적인 배경이 바탕이 되는 것을 느꼈다. 아무쪼록 Policy Gradient를 공부하는 학생에게 도움이 되었으면 좋겠다.
* 혹시 번역된 내용 중에 잘못된 부분이 있으면, 밑의 댓글로 남겨주거나, 메일( kcsgoodboy at gmail dot com or 원저자 lilian dot wengweng at gmail dot com ) 을 주면 감사하겠습니다.
'Study > AI' 카테고리의 다른 글
| [DL] Meta-Learning: Learning to Learn Fast (24) | 2019.07.31 |
|---|---|
| [RL] Temporal Difference Learning : TD(0) (0) | 2019.07.08 |
| [ML] Averaged Perceptron / Pegasos (0) | 2019.07.01 |
| [ML][DS] ColumnTransformer를 활용한 Column Align (0) | 2019.05.30 |
| [RL] (Spinning Up) Proof for Using Q-Function in Policy Gradient Formula (0) | 2019.05.23 |
| [RL] (Spinning Up) Proof for Don't Let the Past Distract You (0) | 2019.05.23 |
| [RL] (Spinning Up) Intro to Policy Optimization (0) | 2019.05.22 |
- Total
- Today
- Yesterday
- 인공지능
- Windows Phone 7
- Expression Blend 4
- 딥러닝
- processing
- Pipeline
- SketchFlow
- 강화학습
- Variance
- TensorFlow Lite
- arduino
- Kinect SDK
- DepthStream
- Gan
- Kinect for windows
- dynamic programming
- Policy Gradient
- Kinect
- Distribution
- RL
- Offline RL
- Off-policy
- windows 8
- 파이썬
- PowerPoint
- 한빛미디어
- End-To-End
- reward
- bias
- ColorStream
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
