 [RL] Q-learning
[RL] Q-learning
강화학습 포스트를 하면서 Bellman Equation을 거쳐 Markov Decision Process까지 오면서 얻어낸 Bellman Equation은 다음과 같다.$$V(s) = \underset{a}{\max}(R(s, a) + \gamma \sum_{s'} P(s,a,s') V(s'))$$ 다시 말해 다음 State의 Value를 계산할 때, 해당 상태에서 특정 행동 a를 취해서 s'로 갈 수 있는 모든 경우의 수를 고려하고 그에 대한 확률의 평균값을 계산해 최대치가 될 수 있는 state의 Value를 구하는게 MDP였다. 그런데 위와 같이 구한 결과 값은 결국 특정 State에 대한 Value를 구한 것이지, 그 Value를 구하는데 있어 행동이 고려된 것이 아니었다. 다시 말해 Agent가..
 [RL] Markov Decision Process (MDP)
[RL] Markov Decision Process (MDP)
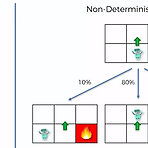
우선 지난 포스트에서도 소개했다시피 Bellman Equation은 각 칸별로 state에 대한 value를 매김으로써 goal까지 가는 최적의 경로를 계산할 수 있었지만, 계산하는 과정에서 확률적인 부분이 고려되지 않아 조금 적용하기 어려운 부분이 있었다. 이 때문에 경로 계산시 확률적인 요소까지 고려한 방법이 이 포스트에서 소개할 Markov Decision Process (MDP)이다. Bellman Equation이 가정했던 것은 왼쪽 그림과 같이 Agent에게 위로 가게끔 하면 Agent는 그 지시에 따라서 위로 움직이게 된다는 것이다. 그런데 이렇게 되면 실질적으로 가르치는 사람이 Agent를 조정하는 형식이 되므로, 학습에 대한 의미가 없어진다. 이때문에 방향 선택에 대해 어느정도의 임의성을..
 [RL] The Bellman Equation
[RL] The Bellman Equation
Richard Ernest Bellman이 제안한 Bellman Equation은 이전 포스트에서 잠깐 소개했던 State와 Action, reward(+ discounted value)를 이용해서 특정 값으로 도출하는 공식으로, 강화학습에서 거의 처음으로 나오는 주제이다. 처음 이 공식이 나왔을 때는 복잡한 조건이 담긴 문제에서 해를 구하는 Dynamic Programming의 기법 중 하나로 쓰였었고, 지금에 이르러서는 강화학습에 많이 활용된다. 이 공식이 어떤식으로 이뤄지는지 간단하게 설명해보고자 한다. 보통 강화학습 강좌를 보면 이런 도식판을 많이 보게 된다. 좌측 하단에는 로봇이 하나가 있고, 우측 상단에는 이 로봇이 도달해야 하는 목표가 있다. 그런데 이 목표의 아래에는 장애물도 하나 있고, ..
- Playing Atari with Deep Reinforcement Learning (Mnih et al, 2013) : 링크 - Hybrid Reward Architecture for Reinforcement Learning (van Seijen et al, 2017) : 링크 - Emergence of Locomotion Behaviors in Rich Enviornments (Heess et al, 2017) : 링크 - Mastering the game of Go without human knowledge (Silver et al, 2017) : 링크
 [RL] Elements of Reinforcement Learning
[RL] Elements of Reinforcement Learning
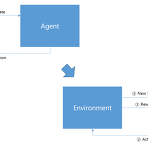
지난 포스트에서도 간단히 소개했지만 강화학습의 구성요소는 다음과 같다. 우선 크게 놓고 보았을때 행동을 하는 주체인 Agent와 행동에 대한 반응을 보여주는 Environment가 있다. Agent는 자신이 취하는 Action을 Environment에게 전달해줄 것이고, 이 Action을 결정하는 근거로써 내부적인 Policy와 Model, Value Function등이 있다. Environment는 Agent로부터 받은 Action에 대한 피드백으로 현재의 state와 옳고 그름을 판단하는 Reward를 Agent에게 전달하는 구조로 되어 있다. 이런 과정이 매 time step마다 이뤄진다. - Time step은 action을 선택하고 state/reward가 Agent에게 전달되는 기본적인 시간 ..
 [RL] Reinforcement Learning
[RL] Reinforcement Learning
보통 아기들이 처음 태어나서 무엇을 할까? 잘 살펴보면 뒤집기, 앉기, 기어가기, 일어서기 까지 일련의 과정을 거친다. 옆에서 지켜보면 그 과정들이 조금 힘겨워 보일 때가 있다. 그런 동작 자체가 아기가 처음 세상 나오면서 처음 경험하는 행동이기 때문에 아기는 주변 사람들이 하는 동작을 보고 따라하려고 노력한다. 우선 아기가 그 동작을 보는 순간 우선 시도를 해볼 것이다. 당연히 처음 해보는 동작인만큼, 그 동작이 정답이 아닐 것이고, 뭔가 잘못된 자세가 나오게 된다. 이때 반복적으로 잘못된 동작을 고치기 위해서 노력할 것이고, 계속 연습을 하게 된다. 결국 동작을 하게 될 것이고, 그때부터는 다양한 주변환경에 대해서도 적응하는 과정도 포함이 될 것이다. 가령 일어서기 과정에서도 '뭔가를 짚고' 일어서는..
 [DL] Convolution의 정의
[DL] Convolution의 정의
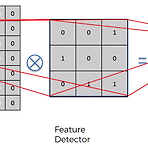
보통 Convolution이라고 사전에서 찾아보면 합성이라는 뜻이 많이 나온다. 그래서 CNN을 합성곱 신경망이라고 표현하는 곳이 많다. 왜 이걸 합성이라고 표현했을까? 사실 전자공학을 전공한 사람이라면 신호처리 수업을 들으면서 많이 들어봤겠지만, 그때의 Convolution은 Linear Time Invariant System상에서 이전값과 현재값을 연산하기 위해 주로 사용하던 연산이다. 의미는 그런식으로 담겨져 있었는데, Convolution Neural Network 상에서는 그런 큰 의미보다는 그냥 이미지내에서 feature를 뽑기 위한 용도로 연산을 활용한다. 일반적으로 다음의 케이스에 대해서 Convolution을 취한다. 위와 같이 어떤 입력 이미지가 들어왔을 때, 여기서 Feature를 감..
 [DL] Convolutional Neural Network이란?
[DL] Convolutional Neural Network이란?
아마 위 그림들을 본 사람이 많을 것이다. 사람이 보기에 따라서 위의 오른쪽 그림은 할머니로도 보일 수 있고, 어떤 사람은 베일을 쓴 여성이 보일 것이다. 또 왼쪽 그림은 사람보기에 따라서 오리로 볼수도 있고, 토끼라고 볼 수 있다. 사실 사람들이 보는 그림의 의미가 다른 이유는 그림이 머리속에 들어왔을 때 뇌가 그렇게 반응하고, 분류를 했기 때문이다. 이 때 뇌는 해당 그림의 feature(특징)을 뽑아보고 기존에 알고 있던 이미지들의 특징과 비교해보면서 그와 유사한 그림을 선택하게 되는 것이다. 위의 그림들에서도 사람들이 보는 결과가 다 다른 이유는 결국 그렇게 뽑아낸 특징이 모호하기 때문인 것이다. Convolutional Neural Network(CNN)은 기존의 Neural Network에서 ..
지난 포스트에서 Dummy Variable Trap을 막기 위해서 모든 Category에 대해서가 아닌 1개를 뺀 만큼만 dummy variable을 만든다고 했었고, 그 의미가 Multicollinearity 인가 뭔가 하는 것때문이라고 했다.(조금 찾아봤는데 Multicollinearity는 다중공선성? 즉 독립변수간의 상관관계를 표현하는 성질이라고 한다.) 이런식으로 불필요한 변수는 제거해야 한다. 사실 지난 포스트는 Categorical Variable를 예로 들어서 설명한 내용이었지만, 일반 Numerical Variable도 동일하다. 학습시킬때 위의 Multicollinearity도 고려해야 하기도 하고, 뭔가 결과를 얻는데 있어서 불필요한 변수는 학습시 배제시켜줘야 한다. 일반 사람이라면 ..
 [ML] Multiple Linear Regression - Intuition
[ML] Multiple Linear Regression - Intuition
지난 포스트에서 다뤘던 simple Linear Regression과 다르게 Multiple Linear Regression은 Independent Variable(IV)가 여러개이다. - Simple Linear Regression : y = b_0 + b_1 * x_1 - Multiple Linear Regression : y = b_0 + b_1 * x_1 + b_2 * x_2 + ... + b_n * x_n그렇기 때문에 지난번에 다뤘던 예제처럼 경력만으로 연봉이 결정되는 극단적인 케이스가 아닌, 여러가지 환경변수를 추가해서 결과에 미치는 영향을 파악할 수 있는 게 Multiple Linear Regression이다. 위의 예제가 앞으로 다룰 예제인데, 여기서 우리는 Dependent Variabl..
 [ML] Simple Linear Regression - Implementation
[ML] Simple Linear Regression - Implementation
이전에 다뤘던 포스트에서 Experience와 Salary간의 Correlation을 구하는 Simple Linear Regression에 대한 설명을 했으니, 실제로 python 코드로 어떻게 구현되는지 살펴보고자 한다. 우선 큰 방향은 다음과 같다.1) 주어진 dataset을 training set과 test set으로 구분한다. 2) training set, test set에 대해서 Linear Regression을 수행한다. 4) 두 결과를 비교한다.1) 주어진 dataset을 training set과 test set으로 구분한다. 이 방법은 이전 포스트에서 다뤘던 것처럼 cross_validation이란 기법을 사용하기 위해서이다. 간단히 말해 주어진 dataset 내에서 학습(training)..
 [ML] Spyder내에서 plot을 new window에 하기
[ML] Spyder내에서 plot을 new window에 하기
아마 열심히 코딩하고 output을 그래프로 많이 뽑을때 matplotlib.pyplot module을 많이 사용할 것이다. 나같은 경우도 다음과 같이 결과값을 plot하려고 했다. 그런데 아마 spyder에 아무 설정을 하지 않은 상태라면 plot이 새로운 창으로 생성되는게 아니라 IPython console로 출력될 것이다. 다음과 같이 말이다.위같이 출력되는 경우도 물론 상관없지만, 아마 그래프를 크게 띄우고 싶어하는 사람이라면 이런 figure가 새로운 창으로 뜨는게 조금더 편할 것이다. 사실 이건 IPython의 Graphic 출력(Graphic Backend)에 대한 설정이 inline으로 되어 있기 때문이다. 이 옵션은 Spyder내에서 Tools-Preference-IPython conso..
 [ML] train_test_split 함수 사용시 DeprecationWarning 없애기
[ML] train_test_split 함수 사용시 DeprecationWarning 없애기
보통 자기가 만든 모델이 맞는지 틀린지를 확인할 때는 cross validation이란 방법을 사용한다. Cross Validation이란 간단히 말해 자신이 가지고 있는 Dataset 내에서 Train Set과 Test Set으로 나눠서 학습시키는 방법이다. python으로 이 방법을 하려면 간단하게 scikit-learn library(sklearn)의 cross_validation module내의 train_test_split이라는 함수를 가져다 쓰면 된다. 실제 사용 방법은 다음과 같다.그런데 언제부터인가 train_test_split을 사용하게 되면 IPython console 창으로 다음과 같은 경고창이 뜨는 것을 확인할 수 있다.C:\ProgramData\Anaconda3\lib\site-p..
 [ML] Simple Linear Regression - Intuition
[ML] Simple Linear Regression - Intuition
Simple Linear Regression이란 말그대로 간단한 Linear Regression, 즉 어떤 dataset 내에서의 어떤 특성을 Linear로 표현하는 과정을 말한다. 다르게 표현하면 data간의 trend line을 긋는다고 표현하기도 한다. 일반적으로 다음과 같은 수식으로 표현하곤 한다. 간단한 선형 방정식인데 여기서 Linear Regression이라고 하는 것은 y와 x_1간의 관계를 찾는 과정이 된다. 그래서 주어진 dataset에서는 x_1의 변화에 따라 y값이 어떻게 변화하는지를 파악하고, 그 와중에 b_0와 b_1이 끼치는 영향을 찾아야 한다. 그래서 y는 x_1의 변화에 따라 변하는 값이라 하여 Dependent Variable(DV)라고 하고, x_1은 Independen..
 [ML] Categorical Variable을 수치화시키기
[ML] Categorical Variable을 수치화시키기
사실 이전 포스트에 이어서 계속하던 작업은 국가와 나이, 연봉의 data를 가지고 이 사람이 물건을 살 것인가 아닌가에 대한 예측을 하기 위한 강의 예제를 따라하고 있었다. 그래서 주어진 dataset을 다시 가져오면 다음과 같다.주어진 field는 4가지 인데, 우리가 구해야 할 결과는 Purchased라고 표기된 부분이고, 이를 위해서 활용해야 할 field는 Country와 Age, Salary field이다. 보통 전자와 같은 자료를 dependent variable, 후자와 같은 자료를 independent variable이라고 말한다. 이중 다른건 모르겠는데 Country field나 Purchased field 같은 경우는 자료가 String 형식으로 되어 있다. 이런 학습에 대해서 잘 모르..
- Total
- Today
- Yesterday
- ai
- Offline RL
- Off-policy
- SketchFlow
- Variance
- 딥러닝
- Expression Blend 4
- 강화학습
- Kinect for windows
- Policy Gradient
- ColorStream
- 파이썬
- processing
- Distribution
- dynamic programming
- Windows Phone 7
- bias
- 한빛미디어
- Kinect SDK
- Kinect
- PowerPoint
- arduino
- reward
- End-To-End
- Gan
- DepthStream
- TensorFlow Lite
- windows 8
- RL
- Pipeline
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |

