티스토리 뷰
(해당 포스트는 Coursera의 Prediction and Control with Function Approximation의 강의 요약본입니다)
역시 Function Approximation 기법을 Monte Carlo Method처럼 TD Learning에다가도 접목시킬 수 있다. 우선 Monte Carlo method에 Function Approximation을 접목한 Gradient Monte Carlo에서 weight이 update되는 과정을 다시 돌아보면 다음과 같다.
$$ \mathbf{w} \leftarrow \mathbf{w} + \alpha[ G_t - \hat{v}(S_t, \mathbf{w})] \nabla \hat{v}(S_t, \mathbf{w}) $$
이를 사용하면 estimate value \(\hat{v}\)이 \(G_t\)에 가까워지게끔 weight이 update되었다. 그럼 여기서 사용된 target인 \(G_t\), 즉 total return 말고 다른 값을 target으로 쓸 수 있을까? 만약 원래의 TD Learning처럼 total return 대신 bootstrapping된 결과, 즉 TD Target을 사용할 수도 있을것이다. 만약 TD Target을 \(U_t\)라고 하면, 아래와 같이
$$ \mathbf{w} \leftarrow \mathbf{w} + \alpha[ U_t - \hat{v}(S_t, \mathbf{w})] \nabla \hat{v}(S_t, \mathbf{w}) $$
만약 이 \(U_t\)가 여러번 뽑아도 동일한 결과가 나올만큼 unbiased하다면, Gradient Monte Carlo method처럼 weight도 어딘가의 local optimum을 찾아갈 것이다. 그런데 아마 TD Target의 형태를 보면,(one-step bootstrapping을 가정했을때)
$$ U_t \doteq R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}) $$
이런 경우는 현재의 estimate된 value를 바탕으로 또 estimate를 하는 경우이므로, 실제값과 많이 차이가 발생할 여지가 생긴다. 다시 말해 bias가 생긴 것이다. 이렇게 되면 이전처럼 local optimum을 찾는다고 보장할 수 없게 된다.
이전과 동일하게 weight의 mean squared error에 대한 gradient를 weight에 관해 취해본다. 그러면 chain rule에 의해서
$$ \nabla \frac{1}{2}[U_t - \hat{v}(S_t, \mathbf{w})]^2 = (U_t - \hat{v}(S_t, \mathbf{w}))(\nabla U_t - \nabla \hat{v}(S_t, \mathbf{w})) $$
라는 값이 나오게 되는데, 위의 식은 TD update를 위한 weight에 관한 식이 아니다. 아마 이상적이라면 \(-(U_t - \hat{v}(S_t, \mathbf{w})) \nabla \hat{v}(S_t, \mathbf{w})\)와 같이 weight의 gradient에 비례한 결과가 나왔어야 하는데, 아래와 같이
$$ (U_t - \hat{v}(S_t, \mathbf{w}))(\color{red}{\nabla U_t} - \nabla \hat{v}(S_t, \mathbf{w})) \neq -(U_t - \hat{v}(S_t, \mathbf{w})) \nabla \hat{v}(S_t, \mathbf{w}) $$
라는 관계를 얻게 되고, 결국 위의 수식이 동등한 것을 보이려면 \(\nabla U_t = 0 \)임을 보여줘야 한다. 그런데 앞에서 정의한 \(U_t\)를 미분해서 취해보면 해당 값은 0이 될 수 없다는 것을 알 수 있다.
$$ \begin{align} \nabla U_t &= \nabla (R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}))\\
&= \gamma \nabla \hat{v}(S_{t+1}, \mathbf{w}) \\ & \neq 0 \end{align}$$
결국 TD learning에서는 Monte Carlo에서 취했던 것처럼 mean squared error에 대한 gradient descent를 통해서 weight를 update할 수 없다는 결론을 낼 수 있다. 간단히 말해서 Gradient Descent처럼 ground truth값이 고정되어야 있는 상황에서 TD learning에서는 TD Target 자체도 weight \(\mathbf{w}\)을 영향을 받기 때문에 bias가 생겨버리게 된다. 그래서 TD estimate에서는 weight의 gradient를 고려하되, TD Target에서는 Target의 gradient를 무시하는 취하는 방법을 취하곤 한다.(이렇게 해야 Target이 계속 변하는 문제를 완화시킬 수 있기에...) 이 방법을 Semi-Gradient(Bootstrapping) method라고 한다. 아래의 알고리즘은 기존의 \(\text{TD}(0)\)에 Semi-Gradient를 적용한 Semi-Gradient \(\text{TD}(0)\)이다.

잘 보면 알겠지만 거의 대부분의 과정이 일반적인 \(\text{TD}(0)\)와 유사하나, 한가지 부분인 weight을 update하기 위해서 TD error를 계산하는 부분에서 gradient는 현재 state \(S\)에서 weight \(\mathbf{w}\)를 가졌을 때의 value function에 대한 gradient만 고려될뿐 next state \(S'\)에 대한 gradient (\(\nabla \hat{v}(S', \mathbf{w})\)) 는 볼 수 없다. 물론 이 semi-gradient방법이 gradient MC처럼 항상 local optimum을 찾거나 그런 보장을 할수는 없지만, 그래도 몇가지 케이스에 대해서는 local optimum을 찾을 수 있고, 무엇보다도 MC에 비해서 TD error를 통해서 매 step 별로 value function을 update할 수 있기 때문에 조금더 빠르게 학습할 수 있다는 장점을 가진다. 굳이 episode가 끝날때까지 기다릴 필요없이, 연속적이고 online으로 학습할 수 있다는 것이다.
궁극적으로 위에서 구한 Semi-Gradient TD와 Gradient MC가 각각 실제 Value function과 어떤 차이를 나타내는지에 대해서는 다음과 같이 그래프로 확인할 수 있다.
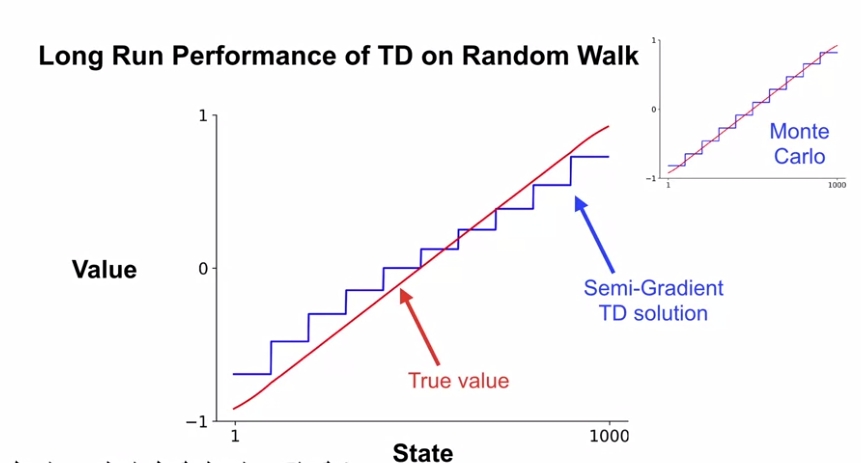
여기에는 State Aggregation도 같이 적용되어 있는데, 앞에서 설명한 바와 같이 Semi-Gradient TD는 Target 자체가 True Value와 같다는 것을 보장할 수 없기 때문에, 위와 같이 Semi-Gradient TD로부터 뽑은 estimate value와 True Value간의 오차가 조금씩 발생한다.
대신 역시 알고 있다시피 Semi-Gradient TD는 일반 TD와 같이 매 step마다 value function update가 이뤄지기 때문에 그만큼 Value Error를 빠르게 줄일 수 있다.
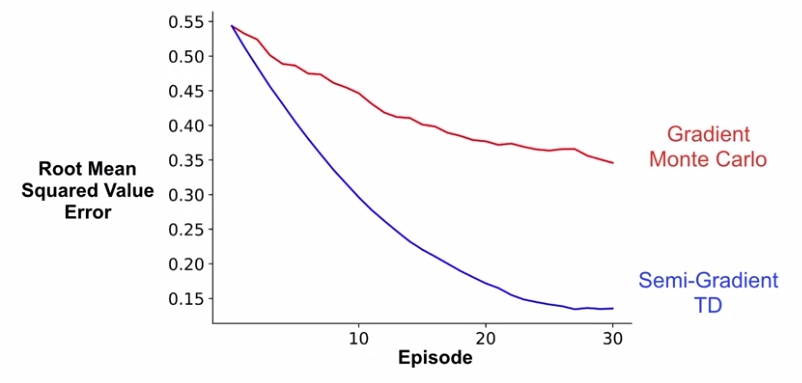
물론 Monte Carlo 방법이 Global optimum을 찾을 수 있는 방법이긴 하지만, 이런 알고리즘을 적용해야 하는 task 마다 performance를 높이는게 중요할 수도 있고, 빨리 학습해서 policy를 개선하는데 의미를 부여할 수 있기 때문에 이때마다 어떤 알고리즘을 선택해야 할지는 고민해볼 일이다.
'Study > AI' 카테고리의 다른 글
| [DL] Pre-Trained Model in OpenVINO (0) | 2020.01.07 |
|---|---|
| [RL] Meta Reinforcement Learning (2) | 2019.11.14 |
| [RL] Linear TD (0) | 2019.11.12 |
| [RL] The Objective for On-policy Prediction (0) | 2019.11.11 |
| [RL] Estimating value function with supervised learning (0) | 2019.11.06 |
| [RL] Dealing with inaccurate models (0) | 2019.10.08 |
| [RL] Dyna as a formalism for planning (3) | 2019.09.30 |
- Total
- Today
- Yesterday
- arduino
- windows 8
- 한빛미디어
- 강화학습
- Expression Blend 4
- dynamic programming
- Policy Gradient
- Pipeline
- SketchFlow
- PowerPoint
- Kinect SDK
- processing
- Off-policy
- Variance
- TensorFlow Lite
- RL
- 딥러닝
- 파이썬
- Distribution
- reward
- Offline RL
- Gan
- Python
- DepthStream
- Kinect for windows
- End-To-End
- Windows Phone 7
- Kinect
- bias
- ColorStream
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
